Could You Explain This Tfw No ZF Joke? I Really Dont Get It... :D
Could you explain this tfw no ZF joke? I really dont get it... :D
Get ready for a long explanation! For everyone’s reference, the joke (supplied by @awesomepus) was:
Q: What did the mathematician say when he encountered the paradoxes of naive set theory?A: tfw no ZF
You probably already know the ‘tfw no gf’ (that feel when no girlfriend) meme, which dates to 2010. I’m assuming you’re asking about the ZF part.
Mathematically, ZF is a reference to Zermelo-Fraenkel set theory, which is a set of axioms commonly accepted by mathematicians as the foundation of modern mathematics. As you probably know if you’ve taken geometry, axioms are super important: they are basic assumptions we make about the world we’re working in, and they have serious implications for what we can and can’t do in that world.
For example, if you don’t assume the Parallel Postulate (that consecutive interior angle measures between two parallel lines and a transversal sum to 180°, or twice the size of a right angle), you can’t prove the Triangle Angle Sum Theorem (that the sum of the angle measures in any triangle is also 180°). It’s not that the Triangle Angle Sum Theorem theorem is not true without the Parallel Postulate — simply that it is unprovable, or put differently, neither true nor false, without that Postulate. Asking whether the Triangle Angle Sum Theorem is true without the Parallel Postulate is really a meaningless question, mathematically. But we understand that, in Euclidean geometry (not in curved geometries), both the postulate and the theorem are “true” in the sense that we have good reason to believe them (e.g., measuring lots of angles in physical parallel lines and triangles). Clearly, the axioms we choose are important.
Now, in the late 19th and early 20th century, mathematicians and logicians were interested in understanding the underpinnings of the basic structures we use in math — sets, or “collections,” being one of them, and arithmetic being another. In short, they were trying to come up with an axiomatic set theory. Cantor and Frege were doing a lot of this work, and made good progress using everyday language. They said that a set is any definable collection of elements, where “definable” means to provide a comprehension (a term you’re familiar with if you program in Python), or rule by which the set is constructed.
But along came Bertrand Russell. He pointed out a big problem in Cantor and Frege’s work, which is now called Russell’s paradox. Essentially, he made the following argument:
Y’all are saying any definable collection is a set. Well, how about this set: R, the set of all sets not contained within themselves. This is, according to you, a valid set, because I gave that comprehension. Now, R is not contained within itself, naturally: if it is contained within itself, then it being an element is a violation of my construction of R in the first place. But R must be contained within itself: if it’s not an element of itself, then it is a set that does not contain itself, and therefore it is an element of itself. So we have that R ∈ R and also R ∉ R. This is a contradiction! Obviously, your theory is seriously messed up.
This paradox is inherently a part of Cantor and Frege’s set theory — it shows that their system was inconsistent (with itself). As Qiaochu Yuan explains over at Quora, the problem is exactly what Russell pointed out: unrestricted comprehension — the idea that you can get away with defining any set you like simply by giving a comprehension. Zermelo and Fraenkel then came along and offered up a system of axioms that formalizes Cantor and Frege’s work logically, and restricts comprehension. This is called Zermelo-Fraenkel set theory (or ZF), and it is consistent (with itself). Cantor and Frege’s work was then retroactively called naive set theory, because it was, of course, pretty childish:

There are two more things worth knowing about axiomatic systems in mathematics. First, some people combine Zermelo-Fraenkel set theory with the Axiom of Choice¹, resulting in a set theory called ZFC. This is widely used as a standard by mathematicians today. Second, Gödel proved in 1931 that no system of axioms for arithmetic can be both consistent and complete — in every consistent axiomatization, there are “true” statements that are unprovable. Or put another way: in every consistent axiomatic system, there are statements which you can neither prove nor disprove.For example, in ZF, the Axiom of Choice is unprovable — you can’t prove it from the axioms in ZF. And in both ZF and ZFC, the continuum hypothesis² is unprovable.³ Gödel’s result is called the incompleteness theorem, and it’s a little depressing, because it means you can’t have any good logical basis for all of mathematics (but don’t tell anyone that, or we might all be out of a job). Luckily, ZF or ZFC has been good enough for virtually all of the mathematics we as a species have done so far!
The joke is that, when confronted with Russell’s paradox in naive set theory, the mathematician despairs, and wishes he could use Zermelo-Fraenkel set theory instead — ‘that feel when no ZF.’
I thought the joke was incredibly funny, specifically because of the reference to ‘tfw no gf’ and the implication that mathematicians romanticize ZF (which we totally do). I’ve definitely borrowed the joke to impress friends and faculty in the math department…a sort of fringe benefit of having a math blog.
– CJH
Keep reading
More Posts from Philosophical-amoeba and Others

I just completed the finishing touches on my new poster, a detailed map of the Mandelbrot Set in a vintage style. I’m calling it the Mandelmap.
The Mandelbrot Set is a fractal shape with infinite detail that you can zoom in on. I often explore the Mandelbrot Set to find trippy patterns to create gifs with, but when I started I felt like I was just poking around at random. So I wanted to create a printed guide for myself to find my way around… I soon realized this was going to be a lot of work, so I decided I might as well take it to the next level and make an awesome poster that would be not just for myself but for everyone else to enjoy too.
What you see here is the result of more than a year’s research, planning, and execution. It’s a 36x24 inch poster rendered fully at 300 dpi, and everything you see was created from scratch. I will be posting more updates and information as I get the test prints in, and I hope to have this poster available to buy within the next couple months!
www.mandelmap.com
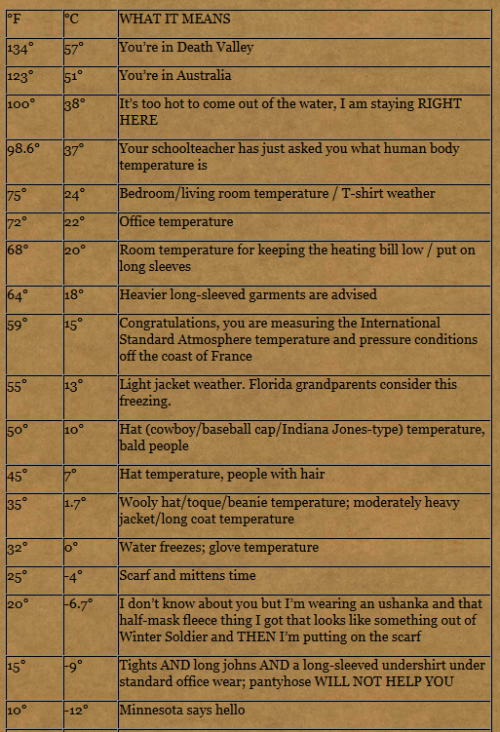

A temperature chart for my fellow Americans who can’t do the Celsius-Fahrenheit equation from memory and for people in the civilized countries who’re too busy making fun of Fahrenheit to do the conversions themselves.






Christ the Redeemer (Portuguese: Cristo Redentor) is an Art Deco statue of Jesus Christ in Rio de Janeiro, Brazil, created by French sculptor Paul Landowski and built by the Brazilian engineer Heitor da Silva Costa, in collaboration with the French engineer Albert Caquot. It is 30 metres (98 ft) tall, not including its 8-metre (26 ft) pedestal, and its arms stretch 28 metres (92 ft) wide.
The statue weighs 635 metric tons (625 long, 700 short tons), and is located at the peak of the 700-metre (2,300 ft) Corcovadomountain in the Tijuca Forest National Park overlooking the city of Rio. As a symbol of Brazilian Christianity, the statue has become an icon for Rio de Janeiro and Brazil. It is made of reinforced concrete and soapstone, and was constructed between 1922 and 1931.
The statue of Christ the Redeemer with open arms, a symbol of peace, was chosen. Local engineer Heitor da Silva Costa designed the statue; it was sculpted by Polish-French sculptor Paul Landowski. Gheorghe Leonida contributed by portraying Jesus Christ’s face on the statue, which made him famous.
A group of engineers and technicians studied Landowski’s submissions and the decision was made to build the structure out of reinforced concrete (designed by Albert Caquot) instead of steel, more suitable for the cross-shaped statue. The outer layers are soapstone, chosen for its enduring qualities and ease of use. Construction took nine years, from 1922 to 1931 and cost the equivalent of US$250,000 ($3,300,000 in 2015). The monument was opened on October 12, 1931.During the opening ceremony, the statue was lit by a battery of floodlights turned on remotely by shortwave radio pioneer Guglielmo Marconi, stationed 5,700 miles (9,200 km) away in Rome.(x)




The Origin of Species by Means of Natural Selection or the Preservation of Favoured Races in the struggle for life Charles Darwin
London John Murray Sixth Edition with additions and corrections (Forty Third Thousand) The sixth edition [shown here] (first printed in 1872) - is the edition in which the word “evolution” was used for the first time (although Darwin used this term in the Descent of Man, published a year before; in 1871). This edition was also the last that Charles Darwin revised during his lifetime, including the addition of an entirely new chapter. In 1876 Darwin added a few small corrections, and all subsequent printing were copies of that printing.
a clean tight fresh presentable copy - which remains largely unread - even after 124 years - a large portion of the book remains unopened [the leaves of the book remain joined at the folds; not slit apart]

Useless Indonesian Chiken facts: Ayam Cemani
Hi tumblr, meet one of the most expensive chiken In the world from Indonesia; Ayam Cemani
No we not paint it black with our excessive coal resources
It simply have unique genes that makes it whole body, meat and even organs all black
It’s chiken so yeah you can eat it, and it said to be very delicous. thou all these years living in Indonesia, I never actually tried it to tell you how it taste
I mean.. It cost up to Rp. 100 Million or about 10.000 USD for one of this chiken…so…..
The extravagant price mostly come from myths that surround these beautiful chiken. said it’ll bring you luck, health and every benefits you can imagine people would said about this emo chiken
pic sc: err…Internet
- J -
-
 myoo-dx liked this · 1 year ago
myoo-dx liked this · 1 year ago -
 reinedesdramess liked this · 1 year ago
reinedesdramess liked this · 1 year ago -
 fragmentednostalgia reblogged this · 6 years ago
fragmentednostalgia reblogged this · 6 years ago -
 helibeb13 liked this · 7 years ago
helibeb13 liked this · 7 years ago -
 haxpaxmax reblogged this · 7 years ago
haxpaxmax reblogged this · 7 years ago -
 recursiverecursion reblogged this · 7 years ago
recursiverecursion reblogged this · 7 years ago -
 lepartiprisdeschoses liked this · 7 years ago
lepartiprisdeschoses liked this · 7 years ago -
 recursiverecursion liked this · 7 years ago
recursiverecursion liked this · 7 years ago -
 just-evo-now liked this · 7 years ago
just-evo-now liked this · 7 years ago -
 sufficientlylargen liked this · 7 years ago
sufficientlylargen liked this · 7 years ago -
 exasperated-24-7 reblogged this · 7 years ago
exasperated-24-7 reblogged this · 7 years ago -
 exasperated-24-7 liked this · 7 years ago
exasperated-24-7 liked this · 7 years ago -
 zuttie-deactivated-2022 reblogged this · 7 years ago
zuttie-deactivated-2022 reblogged this · 7 years ago -
 moonpowered liked this · 7 years ago
moonpowered liked this · 7 years ago -
 pseudomancer liked this · 7 years ago
pseudomancer liked this · 7 years ago -
 ctb1979 liked this · 7 years ago
ctb1979 liked this · 7 years ago -
 secondaristh liked this · 7 years ago
secondaristh liked this · 7 years ago -
 kenyancoder-blog liked this · 7 years ago
kenyancoder-blog liked this · 7 years ago -
 crushdreams liked this · 7 years ago
crushdreams liked this · 7 years ago -
 12x19thefuture liked this · 7 years ago
12x19thefuture liked this · 7 years ago -
 sputnik-schlaeft reblogged this · 7 years ago
sputnik-schlaeft reblogged this · 7 years ago -
 sputnik-schlaeft liked this · 7 years ago
sputnik-schlaeft liked this · 7 years ago -
 enthusiasticindifference liked this · 8 years ago
enthusiasticindifference liked this · 8 years ago -
 r0b0ts-d0nt-have-feel1ngs reblogged this · 8 years ago
r0b0ts-d0nt-have-feel1ngs reblogged this · 8 years ago -
 onions-and-oranges-blog reblogged this · 8 years ago
onions-and-oranges-blog reblogged this · 8 years ago -
 flakopancho liked this · 8 years ago
flakopancho liked this · 8 years ago -
 panpoly-panoply reblogged this · 8 years ago
panpoly-panoply reblogged this · 8 years ago -
 epsilon500 reblogged this · 8 years ago
epsilon500 reblogged this · 8 years ago -
 wmmnola liked this · 8 years ago
wmmnola liked this · 8 years ago -
 curiousvelu liked this · 8 years ago
curiousvelu liked this · 8 years ago -
 phenoct reblogged this · 8 years ago
phenoct reblogged this · 8 years ago -
 unlikeanyoneelse liked this · 8 years ago
unlikeanyoneelse liked this · 8 years ago -
 chizukurowassan liked this · 8 years ago
chizukurowassan liked this · 8 years ago -
 puzzlewocky liked this · 8 years ago
puzzlewocky liked this · 8 years ago -
 iffii liked this · 8 years ago
iffii liked this · 8 years ago -
 willywonka22087-blog liked this · 8 years ago
willywonka22087-blog liked this · 8 years ago -
 phenoct liked this · 8 years ago
phenoct liked this · 8 years ago -
 my-bitterheart liked this · 8 years ago
my-bitterheart liked this · 8 years ago -
 niceg1080 liked this · 8 years ago
niceg1080 liked this · 8 years ago -
 macaroni-hexagon reblogged this · 8 years ago
macaroni-hexagon reblogged this · 8 years ago
A reblog of nerdy and quirky stuff that pique my interest.
291 posts







