13 III 2023
13 III 2023
I remember putting it in my bio a while ago that I dream of doing actual research one day. well this is already happening, as I mentioned in some post, my advisor found an open question for me to write my thesis about
the progress for now is that I'm done with most of the reading I need to do to tackle it and I'm slowly moving forward with thinking of ideas for the solution (or at least a partial one)

this is what I want to do for the rest of my life: reading papers and trying to write my own ones
ofc I don't know if I manage to solve the problem or achieve anything at all with it but the process itself is fun
other than that I've been catching up with homeworks and assignments from work. fortunately I found an MIT lecture recordings for statistics so hopefully I might not die from boredom

watching probability and stats lectures from MIT has been my relationship's idea of netflix and chill for a while now, gotta cultivate the tradition
the algtop professor asked us to write down a full detailed solution for an exercises we did in class, because the person presenting was unable to explain it so I sent him mine


I don't know yet if it's correct but I'm pretty sure it is. I wrote this down partly because who doesn't want extra points and partly because I didn't have a chance to present it, the person who did was faster
I like how my life is right now, I want to keep it that way
More Posts from Bsdndprplplld and Others
27 IV 2022
neglected this place very much, would like to start posting again
may I start with what's new
the last semester was pretty much a failure, I passed everything but my grades were trash. had me seriously doubting my abilities
turns out studying comes easier when I am medicated correctly. I was diagnosed with adhd and asd, so now that I have proper meds and understand my brain a little bit better, things come easier
I fell deeply in love with algebraic topology. there was a notion of excitement about the whole concept of homotopy a few months ago, but now I am fiercely invested in making algebraic topo my field of choice
psychologically I am working on focusing more on the process than the results. it means that my goal is not "to be good at math" but rather to complete this homework, pass that test, etc., in hopes of reducing some of the stress coming from the fear of failure
my current semester is quite boring. ODEs are trivial, yet I have to sit on my ass for a few hours and learn how to solve them. analysis is difficult as always although differential forms are interesting. probability theory is just not my thing. only topology is the light in the tunnel
I don't have any specific plans for the next few days nor do I have any goals. maybe I want to study covering spaces and solve some problems concerning the fundamental group. other than that I need to complete my analysis homework and study de Rham cohomology

here are my category theory notes
tips for studying math
I thought I could share what I learned about studying math so far. it will be very subjective with no scientific sources, pure personal experience, hence one shouldn't expect all of this to work, I merely hope to give some ideas
1. note taking
some time ago I stopped caring about making my notes pretty and it was a great decision – they are supposed to be useful. moreover, I try to write as little as possible. this way my notes contain only crucial information and I might actually use them later because finding things becomes much easier. there is no point in writing down everything, a lot of the time it suffices to know where to find things in the textbook later. also, I noticed that taking notes doesn't actually help me remember, I use it to process information that I'm reading, and if I write down too many details it becomes very chaotic. when I'm trying to process as much as possible in the spot while reading I'm better at structuring the information. so my suggestion would be to stop caring about the aesthetics and try to write down only what is the most important (such as definitions, statements of theorems, useful facts)
2. active learning
do not write down the proof as is, instead write down general steps and then try to fill in the details. it would be perfect to prove everything from scratch, but that's rarely realistic, especially when the exam is in a few days. breaking the proof down into steps and describing the general idea of each step naturally raises questions such as "why is this part important, what is the goal of this calculation, how to describe this reasoning in one sentence, what are we actually doing here". sometimes it's possible to give the proof purely in words, that's also a good idea. it's also much more engaging and creative than passively writing things down. another thing that makes learning more active is trying to come up with examples for the definitions
3. exercises
many textbooks give exercises between definitions and theorem, doing them right away is generally a good idea, that's another way to make studying more active. I also like to take a look at the exercises at the end of the chapter (if that's the case) once in a while to see which ones I could do with what I already learned and try to do them. sometimes it's really hard to solve problems freshly after studying the theory and that's what worked out examples are for, it helps. mamy textbooks offer solutions of exercises, I like to compare the "official" ones with mine. it's obviously better than reading the solution before solving the problem on my own, but when I'm stuck for a long time I check if my idea for the solution at least makes sense. if it's similar to the solution from the book then I know I should just keep going
4. textbooks and other sources
finding the right book is so important. I don't even want to think about all the time I wasted trying to work with a book that just wasn't it. when I need a textbook for something I google "best textbooks for [topic]" and usually there is already a discussion on MSE where people recommend sources and explain why they think that source is a good one, which also gives the idea of how it's written and what to expect. a lot of professors share their lecture/class notes online, which contain user-friendly explenations, examples, exercises chosen by experienced teachers to do in their class, sometimes you can even find exercises with solutions. using the internet is such an important skill
5. studying for exams
do not study the material in a linear order, instead do it by layers. skim everything to get the general idea of which topics need the most work, which can be skipped, then study by priority. other than that it's usually better to know the sketch of every proof than to know a half of them in great detail and the rest not at all. it's similar when it comes to practice problems, do not spend half of your time on easy stuff that could easily be skipped, it's better to practice a bit of everything than to be an expert in half of the topics and unable to solve easy problems from the rest. if the past papers are available they can be a good tool to take a "mock exam" after studying for some time, it gives an opoortunity to see, again, which topics need the most work
6. examples and counterexamples
there are those theorems with statements that take up half of the page because there are just so many assumptions. finding counterexamples for each assumption usually helps with that. when I have a lot of definitions to learn, thinking of examples for them makes everything more specific therefore easier to remember
7. motivation
and by that I mean motivation of concepts. learning something new is much easier if it's motivated with an interesting example, a question, or application. it's easier to learn something when I know that it will be useful later, it's worth it to try to make things more interesting
8. studying for exams vs studying longterm
oftentimes it is the case that the exam itself requires learning some specific types of problems, which do not really matter in the long run. of course, preparing for exams is important, but keep in mind that what really matters is learning things that will be useful in the future especially when they are relevant to the field of choice. just because "this will not be on the test" doesn't always mean it can be skipped
ok I think that's all I have for now. I hope someone will find these helpful and feel free to share yours
1 X 2022
new month huh
yesterday the commutative algebra teacher sent out the first homework assignment. you know, fuck the holiday, we need that grind
I have a week to solve it but I started yesterday as I was so excited

we need to prove some elementary properties of commutative unitary rings and I am enjoying it, I completed a half of the exercises so far. I can tell that the intuition acquired from studying module theory is paying off. many of the requested properties are the special cases of what I encountered during my module venture, so I feel like I understand them quite well. the problem I come across is how to write it down in a rigorous way, but I guess this is why we're supposed to do those exercises
I just got home from the math camp, it was so exhausting. I am not used to being around people all the time, so I my tolerance for interactions is low. I'm glad I went there tho, because I gained some teaching experience – my lecture, choosing contest problems and then grading the solutions
my university offers jobs as graders, older students can make some extra money checking homeworks of younger ones. the requirement is to have a decent GPA, which I don't have so I'm afraid they won't accept me. I don't know how decent exactly tho, so I'm going to try. in particular I might get bonus points for my extracurricular activities, giving talks at conferences and the grading I did at the camp. I'm so done with being poor, I hope I get in. otherwise I might start looking for some programming jobs, not for this academic year but in general, to find out what I could do at all
a few days ago I found a book that I wish I had found sooner: Vector Analysis, Klaus Janich




these are some of the chapters I needed a few months ago for my analysis course. the book is written like a novel and contains many interesting examples. on the bright side there are chapters about riemannian manifolds and other stuff that I haven't yet had an opportunity to study, so I plan to skim through the topics I already know and stay longer at those new to me
well, the sememster starts on tuesday so I don't have much time for that book, but as a sidequest it seems just right
26 IX 2022
I spent the past few days watching good doctor and doing algebra (mostly). I am trying to get used to working in the library

right now I'm at the math camp for the olympiad where I'm giving a lecture on the power of a point and radical axes
I wish I had been in a more math-oriented highschool, I feel like I missed out on so much. my school was focused on literature and philosophy, I switched to math and physics in my last year. on the one hand it's probably a nice achievement that I've managed to get into the university to study math, on the other hand I could have done so much more
I've been struggling to motivate myself to study lately, because the semester starts next week and I cannot really start anything new right now, but I also don't have anything in particular that I could continue. I decided to just read eisenbud and solve some exercises with homology
I read this and it got me thinking that it's funny how many goals and standards people tend to have. my only goals are to have fairly good health and to improve my math skills constantly. maybe it's my obsession, maybe it's the fact that I just gave up long time ago on femininity, social skills, so called emotional intelligence and how I present to other people
besides… why does this sounds like I'm supposed to only date men lmao





Hello, dear! 🌻
I saw your post wanting book recommendations. I'm sorry for your previous struggles, but I hope this list may help you find something you love!
-"The Housekeeper and the Professor" by Yōko Ogawa (The professor is a mathematician!)
-if you like Vonnegut, you may like Haruki Murakami, specifically his older titles like "Wind-Up Bird Chronicle" and "Norwegian Wood" (I feel these books do a good job of expanding on people's motivations and moods.)
-"The Elegance of the Hedgehog" by Muriel Barbery (Again, excellent at conveying emotions.)
-"Hunting and Gathering" by Anna Gavalda (This one is technically a romance - a genre which I personally would normally HATE - but it portrays such realistic characters, their struggles and their natural dialogue during fights that it actually felt more like I was reading about a collection of lives that I had the pleasure of spying on from above. I really love this book!)
-for WWI and WWII-themed titles, I'd recommend the Battlefield comics by Garth Ennis (He's SO good at writing believable characters and realistic dialogues.)
-if you don't mind high fantasy, any of the books in Terry Praychett's Discworld series about the wizards might be up your alley (You can read them independently without issue, or start from the beginning of any of the wizard titles. You can find a reading guide online! The wizards of his world are very regimented about how magic works - somewhat like mathematicians - and it's very funny.)
-the "Cemetery of Forgotten Books" series by Carlos Ruiz Zafón (I'd skip the 4th one - the main character/POV changed and I wasn't as impressed with the writing in that one - but the first 3 books are an absolute dream to read. The characters are so charming, lovable or completely horrifying, it feels like a wonderful foreign mystery series that takes place in 1940s Spain. It was really interesting to try to keep track of such a unique mystery amidst the second world war.)
I hope those help! Please enjoy your reading journey. ♡
hi, and thank you so much for the recommendations! I appreciate it a lot, those books sound really good
10 IX 2022
today I need some extra motivation to study because I didn't sleep well these past few days and it has drastic effects on my productivity, energy, motivation and what have you
also I am struggling to make the choice as to what I should do today
yesterday I started solving some basic exercises from hatcher's textbook



Δ-complex structures are becoming more intuicitve with time. take my solutions with a grain of salt, I am just starting to learn about these things and won't vouch for them lmao



some more complicated objects (the last one is an example of a lense space)
I decided to study commutative algebra today

so far I'm enjoying it. not as much as algebraic topology (which will always be my number 1) but it has its beauty
right now I'm at hom and tensor functors, the structures are fairly complicated, but pretty, and they look like they need to be studied in stages, with repetition and breaks, to fully grasp what's going on
my sensory issues are terrible today and I'm exhausted and hyperactive at the same time uh
I'll try working through a lecture on commutative algebra and give an update on how it went later
update: I studied for a while, but it wasn't going great so I decided to take a nap instead. god knows I tried

The only thing that this university computer-science in-class-use file is dangerous to is my mental health, and the only thing it harms is my soul, but thanks for looking out for me google :)
I have a possibly unusual question. since I left high school and was no longer being forced to read I completely stopped looking at fiction and other books that are not math textbooks. this is partly because I fucking hated reading as an activity – I have adhd and asd, so not only my attention regulation causes a lot of problems, I also struggle with visualizing what's happening and imagining/undestanding the intentions and mindsets of the characters. now, I am properly medicated so attention isn't as much of an issue anymore and I remember enjoying some of the books I've been forced to go through. I miss reading, overall it had a positive impact on my thinking process, I miss analyzing the human experience, so to speak
I liked Dostoyevsky, Vonnegut, Philip K. Dick, Huxley, Kafka and some other "philosophified" authors. I also enjoyed war-themed books in general such as all quiet on the western front, and everything related to the soviet union
finally, my question is, what would you recommend for someone with this taste, who also likes math¹, has a hard time with visual imagination and people but enjoys analyzing human experience, who would possibly like to see a represenation of themselves in the characters of the novel? I would love to rebuild my reading habits, but I am lost as to where to start so I don't get discouraged
¹ I included math in here because maybe there is a book about what it's like to be a mathematician (or a scientist of some kind) that give some existentialist vibes or something, if it exists I want to read it lol
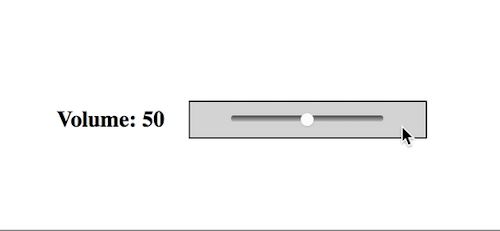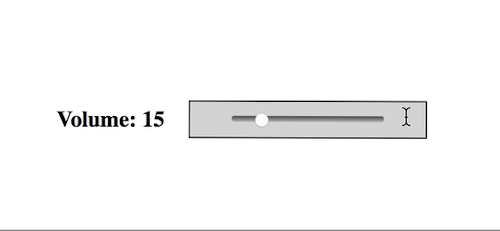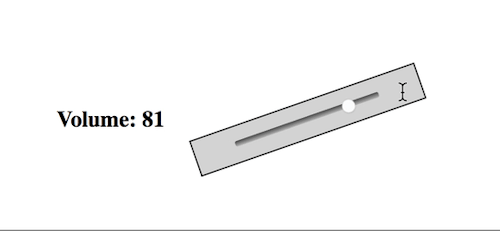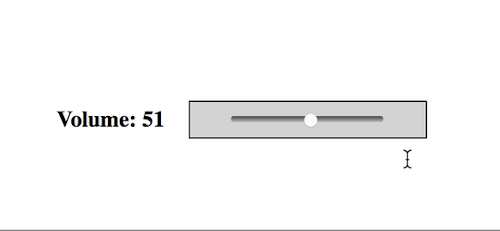
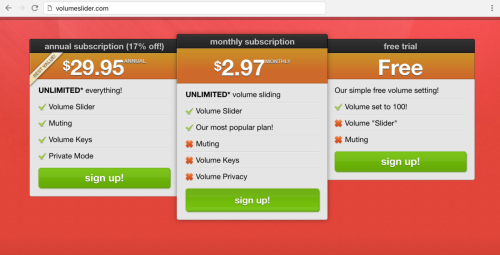
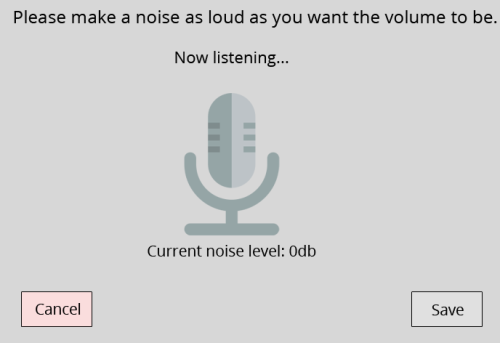
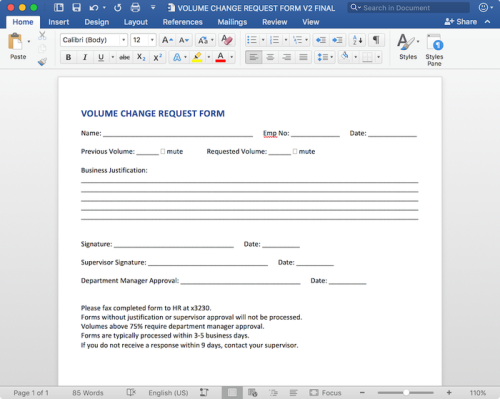
Thank you, /r/ProgrammerHumor, I love you endlessly.
Redditors competing to make the worst volume sliders possible...
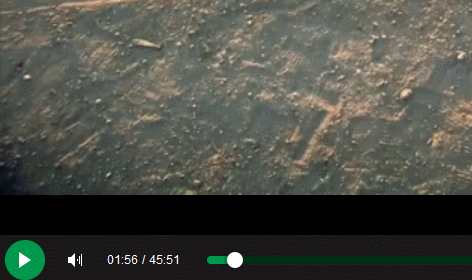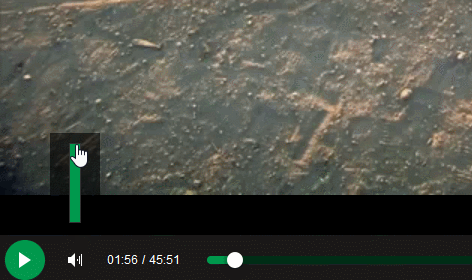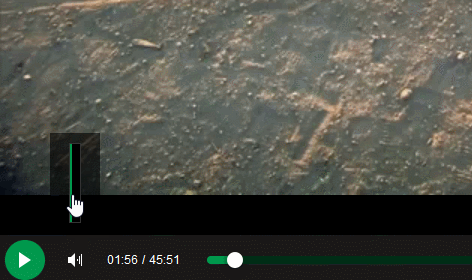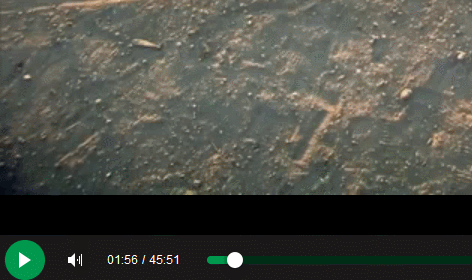




-
 snowdroprd-moved liked this · 2 years ago
snowdroprd-moved liked this · 2 years ago -
 jay-dozed-off liked this · 2 years ago
jay-dozed-off liked this · 2 years ago -
 thenexthat liked this · 2 years ago
thenexthat liked this · 2 years ago -
 ducktoothcollection liked this · 2 years ago
ducktoothcollection liked this · 2 years ago -
 thegrayearloftea liked this · 2 years ago
thegrayearloftea liked this · 2 years ago -
 cinammon-buns liked this · 2 years ago
cinammon-buns liked this · 2 years ago -
 estudieetudie reblogged this · 2 years ago
estudieetudie reblogged this · 2 years ago -
 p-locally liked this · 2 years ago
p-locally liked this · 2 years ago -
 annoyingbasementphantom liked this · 2 years ago
annoyingbasementphantom liked this · 2 years ago -
 notarealwelder liked this · 2 years ago
notarealwelder liked this · 2 years ago -
 luicosas liked this · 2 years ago
luicosas liked this · 2 years ago -
 bsdndprplplld reblogged this · 2 years ago
bsdndprplplld reblogged this · 2 years ago

⁕ pure math undergrad ⁕ in love with anything algebraic ⁕
292 posts