Thank You, /r/ProgrammerHumor, I Love You Endlessly.
Thank you, /r/ProgrammerHumor, I love you endlessly.
Redditors competing to make the worst volume sliders possible...



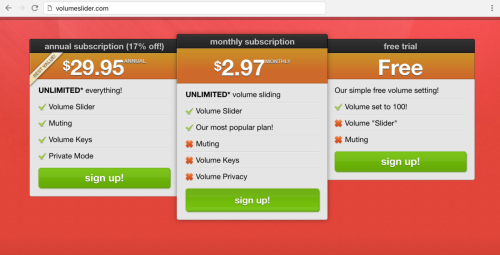

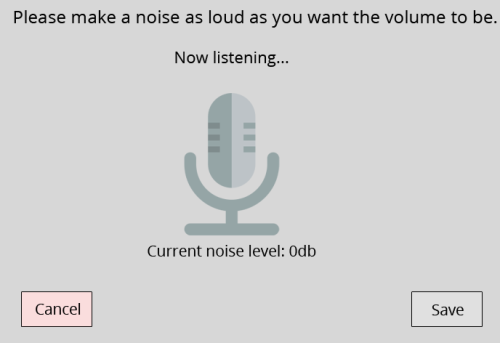
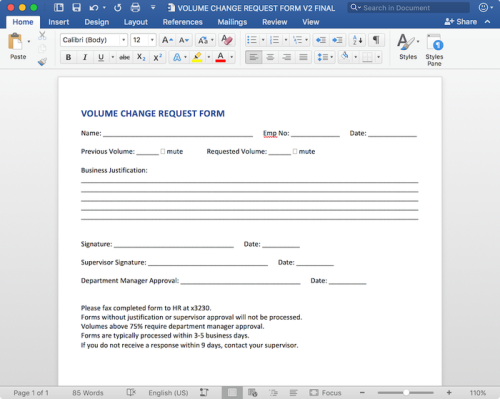
More Posts from Bsdndprplplld and Others

in a way. over the last two years or so. mathematics has become the altar at which I pour out my private grief, and transmute it to something like solace. it does not particularly matter to me if I am ever any good at it. what matters is that the effort I apply to it is rewarded by understanding. I have no natural aptitude for it; I am climbing this hill because it was the steepest and least hospitable to me. there is less agony in the gentler slope, but less valor

[ID: a figure in a textbook that has curved arrows to look like vectors in a field. The figure caption reads, "Is this a vector field? No. It's a picture" /end]
30 VIII 2023
aight it's been a while, time for an update
recently I've been doing mostly algebraic geometry, my advisor gave me some stuff to read, so I'm working through that. the goal is to familiarize myself with hilbert schemes – the topic is advanced, so there are many prerequisites coming up when I'm trying to read the book, that's kinda annoying
we are planning for my thesis to be about a certain generalization of the hilbert scheme, so basically the question is "investigate this space" and I've been having second thoughts whether I'm up for the challenge. I'm just getting to know how all that stuff works, so it's quite overwhelming to see how much I need to learn before I can do anything on my own
nevertheless, I'm pushing through as I will have to learn all of that anyway
I am working on finishing the proof from my bsc thesis and honestly I'm kinda losing hope lmao it turns out that what I probably have to do to complete it is a massive amount of extra reading and an even bigger amount of proving lemmas. the thing is that my work is about something like a generalization of results that have been proven by two people (one of which is khovanov, yes, that khovanov) and I feel it in my balls that the case I'm working on should be treated in a similar way. now the problem is that I can barely understand what they wrote for the "easier" case and I just can't see myself doing that for the more complicated one. oh and for my case I should probably use equivariant cohomology. but all I know about it is the definition, I have never even calculated anything for that + I will do a course on it this semester so it feels futile to study it now. idk I need to talk to my former advisor about this and ask him to be honest, does he even believe that this can be done?
other than that I'm applying for a scholarship. I don't think I will get it, but it is worth trying
I moved in with my boyfriend and our cat decided that my desk is way too big for one person, so now it's our desk

uni starts in a month so I should probably spend that time doing something other than math, which I will be doing all the time once uni starts, but I struggle with coming up with things to do that are not math-related. I should complete some tasks for work, but I would also like to have a hobby
there is a number of things that I could try, for instance reading, drawing, singing, grinding metas for geoguessr (apparently I'm a gamer now), but I can't commit to any of those, my interest comes in waves
maybe I could schedule about an hour per day to do one of those things so that my brain gets used to it. it is not like I can focus on math 24/7, I need to take breaks and I have days when my motivation is zero, so I just sit at my desk and watch stupid shit on youtube. but that's the point, days like that could be spent doing something meaningful and refreshing, instead I just procrastinate math lol
eigenvalues are just the TLDR for a matrix

Just in case some of you don't know about the websites where you can get your textbooks for free

" 'They' isn't singular!" Oh yeah? Show me its multiplicative inverse matrix then.

5x5 Diamond rule, iterates 1-32



Iterates 40, 48, 56

Iterate 64

Iterate 128
This is a 2D cellular automaton generating a 3D fractal layer by layer. I coded it in Microsoft Excel - each pixel is 1 cell.
See more MSExcel fractals
just had a reflection about perfectionism. today I had an exam for which I was prepared very well, but my stupid brain happened and I didn't get the highest grade. my boyfriend was comforting me and he asked since when I want to ace everything, this question made me think
indeed, I don't want to ace everything. I am taking 4 courses this semester, one of which I don't care about enough to strive for the best grade, one of which is way too hard to aim that far, two of which I thought were achievable. and now I didn't achieve that. it feels different to set unrealistic goals and then never achieve them than to set very realistic ones and still fail, that's what I realized today
I am not a perfectionist. I used to be, years ago, and then I learned to set realistic goals. now I'm thinking, isn't perfectionism a kind of a coping mechanism? deep down you know your goals are impossible, so it's not really surprising when you fail. you are never satisfied, sure, but maybe it does feel more safe this way than to not know if you will be satisfied or disappointed. if that's the case then setting realistic goals is absolutely not the way to heal perfectionism
-
 generousparadisephilosopher liked this · 1 week ago
generousparadisephilosopher liked this · 1 week ago -
 farcyber liked this · 1 week ago
farcyber liked this · 1 week ago -
 ginbee liked this · 1 week ago
ginbee liked this · 1 week ago -
 haruspex-md reblogged this · 1 week ago
haruspex-md reblogged this · 1 week ago -
 ofcourseitstrue reblogged this · 1 week ago
ofcourseitstrue reblogged this · 1 week ago -
 iamverysmol liked this · 1 week ago
iamverysmol liked this · 1 week ago -
 azure-luna reblogged this · 1 week ago
azure-luna reblogged this · 1 week ago -
 shinkei-shinto reblogged this · 1 week ago
shinkei-shinto reblogged this · 1 week ago -
 theridiidae reblogged this · 1 week ago
theridiidae reblogged this · 1 week ago -
 strangeandgloriousstarlight reblogged this · 1 week ago
strangeandgloriousstarlight reblogged this · 1 week ago -
 crobody reblogged this · 1 week ago
crobody reblogged this · 1 week ago -
 saiya99 reblogged this · 1 week ago
saiya99 reblogged this · 1 week ago -
 vague-cryptid reblogged this · 1 week ago
vague-cryptid reblogged this · 1 week ago -
 r0b1nexe liked this · 1 week ago
r0b1nexe liked this · 1 week ago -
 of-snow-and-sea liked this · 1 week ago
of-snow-and-sea liked this · 1 week ago -
 truechameleon reblogged this · 1 week ago
truechameleon reblogged this · 1 week ago -
 drella-in-the-bronx reblogged this · 1 week ago
drella-in-the-bronx reblogged this · 1 week ago -
 generousdonkeyskeleton reblogged this · 1 week ago
generousdonkeyskeleton reblogged this · 1 week ago -
 snailor--moon reblogged this · 1 week ago
snailor--moon reblogged this · 1 week ago -
 thetiredyuk reblogged this · 1 week ago
thetiredyuk reblogged this · 1 week ago -
 thetiredyuk liked this · 1 week ago
thetiredyuk liked this · 1 week ago -
 thelittlenoctua reblogged this · 1 week ago
thelittlenoctua reblogged this · 1 week ago -
 thelittlenoctua liked this · 1 week ago
thelittlenoctua liked this · 1 week ago -
 rangerithilien-blog liked this · 1 week ago
rangerithilien-blog liked this · 1 week ago -
 ghostbur-trance reblogged this · 1 week ago
ghostbur-trance reblogged this · 1 week ago -
 boyvains reblogged this · 1 week ago
boyvains reblogged this · 1 week ago -
 boyvains liked this · 1 week ago
boyvains liked this · 1 week ago -
 girlhelpimlostinspace liked this · 2 weeks ago
girlhelpimlostinspace liked this · 2 weeks ago -
 alarastirling reblogged this · 2 weeks ago
alarastirling reblogged this · 2 weeks ago -
 alarastirling liked this · 2 weeks ago
alarastirling liked this · 2 weeks ago -
 thickgatorade08 liked this · 2 weeks ago
thickgatorade08 liked this · 2 weeks ago -
 colossal-idiotx reblogged this · 2 weeks ago
colossal-idiotx reblogged this · 2 weeks ago -
 its-snail-time reblogged this · 2 weeks ago
its-snail-time reblogged this · 2 weeks ago -
 its-snail-time liked this · 2 weeks ago
its-snail-time liked this · 2 weeks ago -
 mortis-sosa liked this · 2 weeks ago
mortis-sosa liked this · 2 weeks ago -
 mrsdelusional liked this · 2 weeks ago
mrsdelusional liked this · 2 weeks ago -
 envys-stories reblogged this · 2 weeks ago
envys-stories reblogged this · 2 weeks ago -
 envys-stories liked this · 2 weeks ago
envys-stories liked this · 2 weeks ago -
 lovvebuggie liked this · 2 weeks ago
lovvebuggie liked this · 2 weeks ago -
 sodaskip reblogged this · 2 weeks ago
sodaskip reblogged this · 2 weeks ago -
 sodaskip liked this · 2 weeks ago
sodaskip liked this · 2 weeks ago -
 nanasboy reblogged this · 2 weeks ago
nanasboy reblogged this · 2 weeks ago -
 nanasboy liked this · 2 weeks ago
nanasboy liked this · 2 weeks ago -
 a-ghost5 liked this · 2 weeks ago
a-ghost5 liked this · 2 weeks ago -
 paralouzer liked this · 2 weeks ago
paralouzer liked this · 2 weeks ago -
 deep-sea-espresso liked this · 2 weeks ago
deep-sea-espresso liked this · 2 weeks ago -
 sketchthetofu liked this · 2 weeks ago
sketchthetofu liked this · 2 weeks ago -
 theskeppticalsystem liked this · 2 weeks ago
theskeppticalsystem liked this · 2 weeks ago -
 peaces-of-magic liked this · 2 weeks ago
peaces-of-magic liked this · 2 weeks ago -
 threetadpolesinatrenchcoat reblogged this · 2 weeks ago
threetadpolesinatrenchcoat reblogged this · 2 weeks ago

⁕ pure math undergrad ⁕ in love with anything algebraic ⁕
292 posts