Yes, This, But Also Among Other Stem Courses In A Typical School, Math Is Taken The Most Seriously. Idk

Me: I should write something

me : … or I could spent 78 hours straight making a miniature library with a working LED chandelier

I have just met you and I love you (via)

req'd by @strictly-script

sure we won't?

text: Abelian't

What's the beef between engineers and physicists and even mathematicians.

Why physicists mock mathematicians: Because playing 51 dimensional chess against your own brain seems silly to us when there’s a whole cosmos to explore.

Why mathematicians mock physicists: The universe can only be understood because some nerd spent the time playing 51 dimensional chess and in the process they created some useful stuff for the physicists to steal and abuse the hell out of.

Why everyone mocks the engineers: π=e=3 is an abomination before God and those pencil pushing dorks make more money than us so we feel the need to vindicate our $75000 student debt.

my love for topology is a very concave function with a very positive derivative

tietze theorem is fucking beautiful urysohn's lemma is pretty and separation axioms are cute

aand i animated some riemann integration today:

i could've chosen different partitions or a different function in order to achieve more frames but i like this anyway

the alphabet is like, there's the "a" region (abc...), for just, things, there's the "f" region (fgh..), for functions, there's the "i" region (ijk...), for indices, there's the "n" region (nm...), for integers, and the "p" region (pq...), for integers that are prime, there's the "t" region (tsr...), for time and progression and other axes that aren't the usual ones, and then there's the "u" region (uv...), for like, i guess open sets and differentiable functions and the such i guess, and then finally there's the "x" region (xyzw...) for just, variables that are more variable-y

there's also o and l but you shouldn't use those

tips for studying math

I thought I could share what I learned about studying math so far. it will be very subjective with no scientific sources, pure personal experience, hence one shouldn't expect all of this to work, I merely hope to give some ideas

1. note taking

some time ago I stopped caring about making my notes pretty and it was a great decision – they are supposed to be useful. moreover, I try to write as little as possible. this way my notes contain only crucial information and I might actually use them later because finding things becomes much easier. there is no point in writing down everything, a lot of the time it suffices to know where to find things in the textbook later. also, I noticed that taking notes doesn't actually help me remember, I use it to process information that I'm reading, and if I write down too many details it becomes very chaotic. when I'm trying to process as much as possible in the spot while reading I'm better at structuring the information. so my suggestion would be to stop caring about the aesthetics and try to write down only what is the most important (such as definitions, statements of theorems, useful facts)

2. active learning

do not write down the proof as is, instead write down general steps and then try to fill in the details. it would be perfect to prove everything from scratch, but that's rarely realistic, especially when the exam is in a few days. breaking the proof down into steps and describing the general idea of each step naturally raises questions such as "why is this part important, what is the goal of this calculation, how to describe this reasoning in one sentence, what are we actually doing here". sometimes it's possible to give the proof purely in words, that's also a good idea. it's also much more engaging and creative than passively writing things down. another thing that makes learning more active is trying to come up with examples for the definitions

3. exercises

many textbooks give exercises between definitions and theorem, doing them right away is generally a good idea, that's another way to make studying more active. I also like to take a look at the exercises at the end of the chapter (if that's the case) once in a while to see which ones I could do with what I already learned and try to do them. sometimes it's really hard to solve problems freshly after studying the theory and that's what worked out examples are for, it helps. mamy textbooks offer solutions of exercises, I like to compare the "official" ones with mine. it's obviously better than reading the solution before solving the problem on my own, but when I'm stuck for a long time I check if my idea for the solution at least makes sense. if it's similar to the solution from the book then I know I should just keep going

4. textbooks and other sources

finding the right book is so important. I don't even want to think about all the time I wasted trying to work with a book that just wasn't it. when I need a textbook for something I google "best textbooks for [topic]" and usually there is already a discussion on MSE where people recommend sources and explain why they think that source is a good one, which also gives the idea of how it's written and what to expect. a lot of professors share their lecture/class notes online, which contain user-friendly explenations, examples, exercises chosen by experienced teachers to do in their class, sometimes you can even find exercises with solutions. using the internet is such an important skill

5. studying for exams

do not study the material in a linear order, instead do it by layers. skim everything to get the general idea of which topics need the most work, which can be skipped, then study by priority. other than that it's usually better to know the sketch of every proof than to know a half of them in great detail and the rest not at all. it's similar when it comes to practice problems, do not spend half of your time on easy stuff that could easily be skipped, it's better to practice a bit of everything than to be an expert in half of the topics and unable to solve easy problems from the rest. if the past papers are available they can be a good tool to take a "mock exam" after studying for some time, it gives an opoortunity to see, again, which topics need the most work

6. examples and counterexamples

there are those theorems with statements that take up half of the page because there are just so many assumptions. finding counterexamples for each assumption usually helps with that. when I have a lot of definitions to learn, thinking of examples for them makes everything more specific therefore easier to remember

7. motivation

and by that I mean motivation of concepts. learning something new is much easier if it's motivated with an interesting example, a question, or application. it's easier to learn something when I know that it will be useful later, it's worth it to try to make things more interesting

8. studying for exams vs studying longterm

oftentimes it is the case that the exam itself requires learning some specific types of problems, which do not really matter in the long run. of course, preparing for exams is important, but keep in mind that what really matters is learning things that will be useful in the future especially when they are relevant to the field of choice. just because "this will not be on the test" doesn't always mean it can be skipped

ok I think that's all I have for now. I hope someone will find these helpful and feel free to share yours

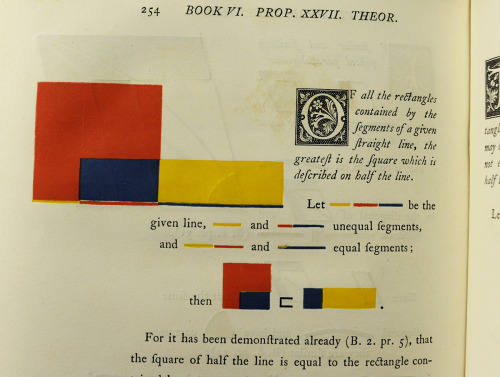
The beautiful modernism of Oliver Byrne’s, The First Six Books of the Elements of Euclid, 1847

that's an interesting perspective

recently I've been thinking about it in an opposite way. it started during a conversation about brains, in particular how stupid and flawed they are, I realized that I enjoy math because it gives me a break from being human. there is no place for emotion and cognitive bias, only formal reasoning and proofs. it feels so safe and so distant from the day-to-day life filled with problems caused by the human nature, it feels so clean. it's a place for me to enjoy only the best qualities of my existence. it's an acceptable way to separate myself from everyone, and simultaneously stay connected

I love how different this is from what is described above, as if math offered a place for everyone to find something that they will like

Im trying to find a really long Tumblr post that talked about how sad it was that people are so happy to complain about how much they hated math and how math can be a way to connect with your fundamental humanity and...

Yeah, I've been studying a little bit of it on my own, ten years after I dropped out of college, I've been going back to seeing some basics of calculus, and I've been really feeling some of that.

There is this sense that math is this alien thing, separate from the true concerns of humanity. This external topic, strange and inhumane that only those few weirdos with a eccentric and atypical cast of mind, who are themselves separate by a few degrees from human nature, can grasp.

But it's not that, We, messy warm emotional dumb humans came up with it, we silly atavistic creatures dedicated so much time and effort to develop it and explore it, this silly, quirky, wet, ape-like species is the only living creature on this planet that concerns itself with doing math in any serious capacity. It didn't come from aliens or the gods or from dolphins, math came from humans and humans are the only ones that use them. There could be nothing more human, more fundamentally ours, more intrinsic to our nature than math.

And it's not just a tool! Is not just this thing to be celebrated because its useful in a purely base pragmatical, prosaic way. Is not this thing we have to dissapasionatly conceed credit to because I guess it does useful things like bridges and rockets and computers and taxes. Math is not just the civilizational equivalent of going to the dentist or eating your vegetables.

i hesitate to call it a philosophy or an art, it is a way of human thinking, it is a way of thinking like a human, of thinking in a way that only humans can think. its is one of our oldest and proudest traditions, it is a way to feel greater than onself, it is a way of growing. it is a song with a prosody all its own. There is such a profound sense of meaning and beauty and truth and purpose to be found in math, and the best of all is that it works, when it says something it means something, its telling you a thing that is meaningful, that represents something true, that couldnt be any other way, that has consequences and uses and can be relied upon, that it representes something which carries weight and its ours, its truly a part of our nature, of what we are.

Complex Number Grapher

https://jutanium.github.io/ComplexNumberGrapher/

This grapher is really fun to play around with! 

A normal function takes in a number, x, and outputs another number, y. But a complex function takes in a complex point on a plane (a+bi) and outputs another complex point. Without 4 dimensions, it would be impossible to graph a complex function :(

The creator of this project instead uses complex domain coloring which they explain much better than I have here so you should 100% go and check it out!

Look at this cool function I got:

f(z)=(sin(z^3))^((cos(z))/2)