Hey Guys Quick Question

at some point I was wondering what about the researcher publishing their paper in an expensive journal and it turns out that the author does not make a lot of money from that, so it really is about fucking this exploitative system and not doing any substantial harm to the researcher, if anyone was worrying like I was

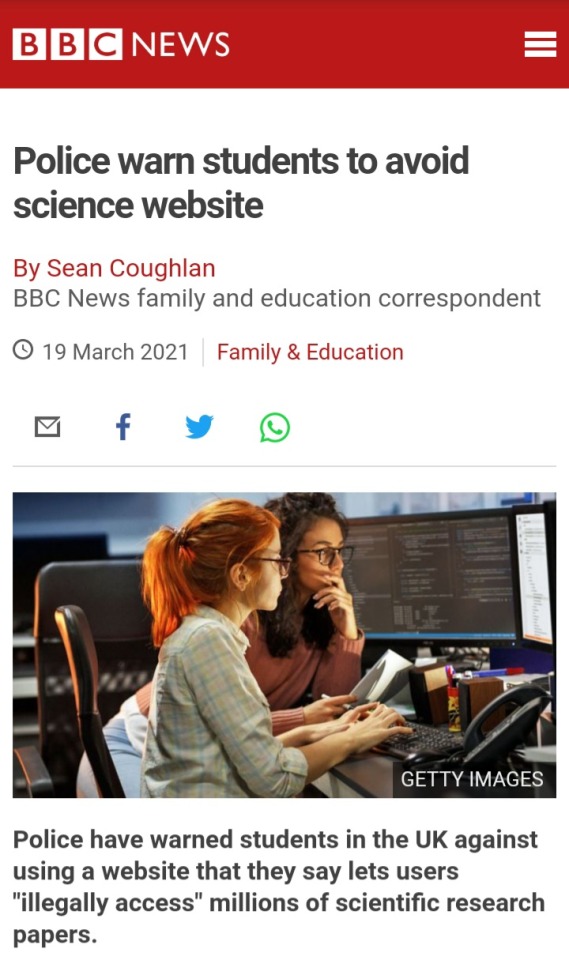
This is about Sci-Hub. yeah we get it.. gatekeep knowledge and protect the interests of capital…

31 VII 2022

finally posting after the exams are over, it was the longest session I have ever experienced, a month of exams. I passed everything and it was a good semester, actually my grades are better than ever before, which comes off as a surprise, I can't believe that it's anything other than luck

now what am I going to do for the holiday huh

next semester I am going to take three courses: analytic functions, commutative algebra and a mix-course of category theory, sheaf theory and homological algebra. then I plan to take algebraic topology, algebraic geometry, number theory and some more abstract algebra, along with writing a bachelor's thesis. this is probably going to be the hardest year so far, I don't know how I am going to survive this, I'm so scared

I was asked to give some lectures on geometry during a math summer camp for people who want to participate in the math olympiad. it's a great opportunity for me to practice giving lectures, as that's what I plan my job to be. moreover, it is my dream to be so good at math that I could prep people for the olympiad, hence that's a fraction of that dream coming true

the problem is I don't know geometry lol last time I did any was like four years ago in high school

thus I play with triangles everyday

other than that I must prepare a talk for a conference, I chose to do one on the knot theory, Seifert surfaces specifically. I started reading about it some time ago and it seems super cool

untangling knots is a perfect thing to do for fun

my plan for the holiday outside of these side-quests is to learn as much as possible for the courses that I'll be taking. the problem with them (besides analytic functions) is that they will be quite technical, detailed and dry, as they are supposed to give the tools necessary to study algebraic topology and geometry. that does sound dreadfully boring, no? that's what scares me, because when I am not interested in what I'm trying to learn everything becomes twice as hard. I asked here and there for advice and people told me to read about algebraic geometry in tandem with commutative algebra, since many constructions have beautiful interpretations and motivations there. sounds like exactly what I need

my bachelor's thesis will be on algebraic or differential topology probably, but I don't know exactly what I want to write about. I was thinking about vector fields on manifolds or de rham cohomology, but the thing with the proseminar on geometric topology (mine) is that it's been planned to give the introduction to the currently researched topics and offer opportunities to work with fresh conjectures and theorems. at least that's how it was described. allegedly geometric topology has this property that undergrads can contribute to the development of new theory, which is very surprising to me ngl, I would guess that this is highly unlikely with any kind of math nowadays and yet here we are

in conclusion, I'm excited but scared

tips for studying math

I thought I could share what I learned about studying math so far. it will be very subjective with no scientific sources, pure personal experience, hence one shouldn't expect all of this to work, I merely hope to give some ideas

1. note taking

some time ago I stopped caring about making my notes pretty and it was a great decision – they are supposed to be useful. moreover, I try to write as little as possible. this way my notes contain only crucial information and I might actually use them later because finding things becomes much easier. there is no point in writing down everything, a lot of the time it suffices to know where to find things in the textbook later. also, I noticed that taking notes doesn't actually help me remember, I use it to process information that I'm reading, and if I write down too many details it becomes very chaotic. when I'm trying to process as much as possible in the spot while reading I'm better at structuring the information. so my suggestion would be to stop caring about the aesthetics and try to write down only what is the most important (such as definitions, statements of theorems, useful facts)

2. active learning

do not write down the proof as is, instead write down general steps and then try to fill in the details. it would be perfect to prove everything from scratch, but that's rarely realistic, especially when the exam is in a few days. breaking the proof down into steps and describing the general idea of each step naturally raises questions such as "why is this part important, what is the goal of this calculation, how to describe this reasoning in one sentence, what are we actually doing here". sometimes it's possible to give the proof purely in words, that's also a good idea. it's also much more engaging and creative than passively writing things down. another thing that makes learning more active is trying to come up with examples for the definitions

3. exercises

many textbooks give exercises between definitions and theorem, doing them right away is generally a good idea, that's another way to make studying more active. I also like to take a look at the exercises at the end of the chapter (if that's the case) once in a while to see which ones I could do with what I already learned and try to do them. sometimes it's really hard to solve problems freshly after studying the theory and that's what worked out examples are for, it helps. mamy textbooks offer solutions of exercises, I like to compare the "official" ones with mine. it's obviously better than reading the solution before solving the problem on my own, but when I'm stuck for a long time I check if my idea for the solution at least makes sense. if it's similar to the solution from the book then I know I should just keep going

4. textbooks and other sources

finding the right book is so important. I don't even want to think about all the time I wasted trying to work with a book that just wasn't it. when I need a textbook for something I google "best textbooks for [topic]" and usually there is already a discussion on MSE where people recommend sources and explain why they think that source is a good one, which also gives the idea of how it's written and what to expect. a lot of professors share their lecture/class notes online, which contain user-friendly explenations, examples, exercises chosen by experienced teachers to do in their class, sometimes you can even find exercises with solutions. using the internet is such an important skill

5. studying for exams

do not study the material in a linear order, instead do it by layers. skim everything to get the general idea of which topics need the most work, which can be skipped, then study by priority. other than that it's usually better to know the sketch of every proof than to know a half of them in great detail and the rest not at all. it's similar when it comes to practice problems, do not spend half of your time on easy stuff that could easily be skipped, it's better to practice a bit of everything than to be an expert in half of the topics and unable to solve easy problems from the rest. if the past papers are available they can be a good tool to take a "mock exam" after studying for some time, it gives an opoortunity to see, again, which topics need the most work

6. examples and counterexamples

there are those theorems with statements that take up half of the page because there are just so many assumptions. finding counterexamples for each assumption usually helps with that. when I have a lot of definitions to learn, thinking of examples for them makes everything more specific therefore easier to remember

7. motivation

and by that I mean motivation of concepts. learning something new is much easier if it's motivated with an interesting example, a question, or application. it's easier to learn something when I know that it will be useful later, it's worth it to try to make things more interesting

8. studying for exams vs studying longterm

oftentimes it is the case that the exam itself requires learning some specific types of problems, which do not really matter in the long run. of course, preparing for exams is important, but keep in mind that what really matters is learning things that will be useful in the future especially when they are relevant to the field of choice. just because "this will not be on the test" doesn't always mean it can be skipped

ok I think that's all I have for now. I hope someone will find these helpful and feel free to share yours

can someone please get these hoes under control i'm BUSY

no fuckin way

tips for studying math part 2:

studying for an exam but the course is super boring and you don't care about it at all, you just want to pass

start by making a list of topics that were covered in lectures and classes. you can try to sort them by priority, maybe the professor said things like "this won't be on the exam" or "this is super important, you all must learn it", but that's not always possible, especially if you never showed up in class. instead, you can make a list of skills that you should acquire, based on what you did in classes and by looking at the past papers. for example, when I was studying for the statistics exam, my list of skills included things such as calculating the maximum likelihood estimators, confidence intervals, p-values, etc.

normally it is recommended to take studying the theory seriously, read the proofs, come up with examples, you name it, but we don't care about this course so obviously we are not going to do that. after familiarizing yourself with the definitions, skim through the lecture notes/slides/your friend's notes and try to classify the theorems into actionable vs non-actionable ones. the actionable ones tell you directly how to calculate something or at least that you can do it. the stokes theorem or the pappus centroid theorem – thore are really good examples of that. they are the most important, because chances are you used them a lot in class and they easily create exam problems. the non-actionable theorems tell you about properties of objects, but they don't really do anything if you don't care about the subject. you should know them of course, sometimes it is expected to say something like "we know that [...] because the assumptions of the theorem [...] are satisfied". but the general rule of thumb is that you should focus on the actionable theorems first.

now the problem practice. if you did a lot of problems in class and you have access to past papers, then it is pretty easy to determine how similar those two are. if the exercises covered in class are similar to those from past exam papers, then the next step is obvious: solve the exercises first, then work on the past papers, and you should be fine. but this is not always the case, sometimes the classes do not sufficiently prepare you for the exam and then what you do is google "[subject] exercises/problems with solutions pdf". there is a lof of stuff like this online, especially if the course is on something that everybody has to go through, for instance linear algebra, real and complex analysis, group theory, or general topology. if your university offers free access to textbooks (mine does, we have online access to some books from springer for example) then you can search again "[subject] exercises/problems with solutions". of course there is the unethical option, but I do not recommend stealing books from libgen by searching the same phrase there. once you got your pdfs and books, solve the problems that kinda look like those from the past papers.

if there is a topic that you just don't get and it would take you hours to go through it, skip it. learn the basics, study the solutions of some exercises related to it, but if it doesn't go well, you can go back to it after you finish the easy stuff. it is more efficient to learn five topics during that time than to get stuck on one. the same goes for topics that were covered in lectures but do not show up on the past papers. if you don't have access to the past papers you gotta trust your intuition on whether the topic looks examable or not. sometimes it can go wrong, in particular when you completely ignored the course's existence, but if you cannot find any exercises that would match that topic, then you can skip it and possibly come back later. always start with what comes up the most frequently on exams and go towards what seems the most obscure. if your professor is a nice person, you can ask them what you should focus on and what to do to prepare, that can save a lot of time and stress.

talk to the people who already took the course. ask them what to expect – does the professor expect your solutions to be super precise and cuts your points in half for computation errors or maybe saying that the answer follows from the theorem X gets the job done? normally this wouldn't be necessary (although it is always useful to know these things) because when you care about the course you are probably able to give very nice solutions to everything or at least that's your goal. but this time, if many people tell you that the professor accepts hand-wavey answers, during the exam your tactic is to write something for every question and maybe you'll score some extra points from the topics you didn't have time to study in depth.

alright, that should do it, this is the strategy that worked for me. of course some of those work also in courses that one does care about, but the key here is to reduce effort and time put into studying while still maximizing the chances of success. this is how I passed statistics and differential equations after studying for maybe two days before each exam and not attending any lectures before. hope this helps and of course, feel free to add yours!

I know we all have different skills and all and it's supposed to be complementary, but, people who can do math are so morbidly funny to me

I figure it must be like

Imagine being like only one of twelve people in your whole city who can read and write

And it's not just because everyone else is uneducated, most of them cannot even learn the sort of things you can learn. Or they could, in theory, but it frustrates them so much that they never make it past grade school reading tops, and they hate every second of it

And it's not a "luxury" skill, either, like your whole society needs the written word to function, and by extension, they need you. They need you for shit like reading labels and instruction manuals and writting 2 sentences letters, and they pay you handsomely for that, which is nice, but also feels absurd

You read a whole series of novels that rock your life and you can't even talk about it to your best friend because anything more complex than a picture book breaks their brain

Here’s a long but important comic for you <3

Accepting ourselves the way we are means we allow ourselves the things we need to make life a little easier. You don’t have to fight it, it’s ok have different needs to others. You are worthy of kindness, so be kind to you <3

love from the sad ghost club <3

Shop / About Us / FAQ’s / comics / Archive / Subscribe / Theme

To all the people wondering how to do proofs: A good place to start is to read "Book of Proof" by Richard Hammack. Just Google it, it's completely free and available online!

Yes! Also, for people just curious about mathematical proofs, who want to kind of see what they're like I suggest 'Proofs from the book' by Martin Aigner and Günter M. Ziegler. A short summary of this book is some of the most beautiful mathematical proofs from a range of mathematical fields. You may not understand it fully as a layman but it can be an interesting look into proofs.

Here is a free link to the 5th edition of the book

DO YOU KNOW WHAT I JUST REALIZED

YOU KNOW THE HAIKU BOT???

OFC YOU DO

YOU KNOW THAT MESSAGE HE PUTS AT THE END OF EVERY POST????

"Beep boop! I look for accidental haiku posts. Sometimes I mess up."

YEAH???????

WELL THATS A HAIKU TOO

Beep boop! I look for

accidental haiku posts.

Sometimes I mess up.

NOW YOU LOOK ME IN THE EYE AND TELL ME THATS NOT THE CUTEST THNIG YOUVE EVER HEARD