Tips For Studying Math Part 2:

rb this with ur opinion on this shade of pink:

Real estate agent, 5 minutes into the meeting with a topologist: So, when you were talking about "contracting" a "house with two rooms",

Mathematics: What do grad students in math do all day?

Mathematics: What do grad students in math do all day? - gist:4158578

“A lot of math grad school is reading books and papers and trying to understand what’s going on. The difficulty is that reading math is not like reading a mystery thriller, and it’s not even like reading a history book or a New York Times article.

The main issue is that, by the time you get to the frontiers of math, the words to describe the concepts don’t really exist yet. Communicating these ideas is a bit like trying to explain a vacuum cleaner to someone who has never seen one, except you’re only allowed to use words that are four letters long or shorter.

What can you say?

“It is a tool that does suck up dust to make what you walk on in a home tidy.”

That’s certainly better than nothing, but it doesn’t tell you everything you might want to know about a vacuum cleaner. Can you use a vacuum cleaner to clean bookshelves? Can you use a vacuum cleaner to clean a cat? Can you use a vacuum cleaner to clean the outdoors?

The authors of the papers and books are trying to communicate what they’ve understood as best they can under these restrictions, and it’s certainly better than nothing, but if you’re going to have to work with vacuum cleaners, you need to know much more.

Fortunately, math has an incredibly powerful tool that helps bridge the gap. Namely, when we come up with concepts, we also come up with very explicit symbols and notation, along with logical rules for manipulating them. It’s a bit like being handed the technical specifications and diagrams for building a vacuum cleaner out of parts.

The upside is that now you (in theory) can know 100% unambiguously what a vacuum cleaner can or cannot do. The downside is that you still have no clue what the pieces are for or why they are arranged the way they are, except for the cryptic sentence, “It is a tool that does suck up dust to make what you walk on in a home tidy.”

OK, so now you’re a grad student, and your advisor gives you an important paper in the field to read: “A Tool that does Suck Dust.” The introduction tells you that “It is a tool that does suck up dust to make what you walk on in a home tidy,” and a bunch of other reasonable but vague things. The bulk of the paper is technical diagrams and descriptions of a vacuum cleaner. Then there are some references: “How to use air flow to suck up dust.” “How to use many a coil of wire to make a fan spin very fast.” “What you get from the hole in the wall that has wire in it.”

So, what do you do? Technically, you sit at your desk and think. But it’s not that simple. First, you’re like, lol, that title almost sounds like it could be sexual innuendo. Then you read the introduction, which pleasantly tells you what things are generally about, but is completely vague about the important details.

Then you get to the technical diagrams and are totally confused, but you work through them piece by piece. You redo many of the calculations on your own just to double check that you’ve really understood what’s going on. Sometimes, the calculations that you redo come up with something stupid, and then you have to figure out what you’ve understood incorrectly, and then reread that part of the technical manual to figure things out. Except sometimes there was a typo in the paper, so that’s what screwed things up for you.

After a while, things finally click, and you finally understand what a vacuum cleaner is. In fact, you actually know much more: You’ve now become one of the experts on vacuum cleaners, or at least on this particular kind of vacuum cleaner, and you know a good fraction of the details on how it works. You’re feeling pretty proud of yourself, even though you’re still a far shot from your advisor: They understand all sorts of other kinds of vacuum cleaners, even Roombas, and, in addition to their work on vacuum cleaners, they’re also working on a related but completely different project about air conditioning systems.

You are filled with joy that you can finally talk on par with your advisor, at least on this topic, but there is a looming dark cloud on the horizon: You still need to write a thesis.

So, you think about new things that you can do with vacuum cleaners. So, first, you’re like: I can use a vacuum cleaner to clean bookshelves! That’d be super-useful! But then you do a Google Scholar search and it turns out that someone else did that like ten years ago.

OK, your next idea: I can use a vacuum cleaner to clean cats! That’d also be super-useful. But, alas, a bit more searching in the literature reveals that someone tried that, too, but they didn’t get good results. You’re a confident young grad student, so you decide that, armed with some additional techniques that you happen to know, you might fix the problems that the other researcher had and get vacuuming cats to work. You spend several months on it, but, alas, it doesn’t get you any further.

OK, so then, after more thinking and doing some research on extension cords, you think it would be feasible to use a vacuum cleaner to clean the outdoors. You look in the literature, and it turns out that nobody’s ever thought of doing that! You proudly tell this idea to your advisor, but they do some back of the envelope calculations that you don’t really understand and tell you that vacuuming the outdoors is unlikely to be very useful. Something about how a vacuum cleaner is too small to handle the outdoors and that we already know about other tools that are much better equipped for cleaning streets and such.

This goes on for several years, and finally you write a thesis about how if you turn a vacuum cleaner upside-down and submerge the top end in water, you can make bubbles!

Your thesis committee is unsure of how this could ever be useful, but it seems pretty cool and bubbles are pretty, so they think that maybe something useful could come out of it eventually. Maybe.

And, indeed, you are lucky! After a hundred years or so, your idea (along with a bunch of other ideas) leads to the development of aquarium air pumps, an essential tool in the rapidly growing field of research on artificial goldfish habitats. Yay!”

saving this for self-care and for anyone who might need this

also, I can add: squint your eyes hard and then looking at something far away. it's supposed to help your eyes relax and a bonus simple grounding exercise!

from my personal experience, once you start paying attention to how different it feels on your eyes to look at something far away as opposed to something close, you can relax your eyes without needing an object to look at. now when I'm going to bed I imagine a tree far away and I feel my eyes relaxing, it helps with me fall alseep faster. it might be a placebo ofc, I know nothing about eyes, but it is still a good trick for falling asleep regardless of the supposed effect of it on the eyes

We need like “unclench your jaw” posts but for eye strain. Like

Go look at something 20ft away for 20 seconds.

(Points at the function I'm doing my thesis on) this is my son who has every disease

Visualization of the Rubik's cube

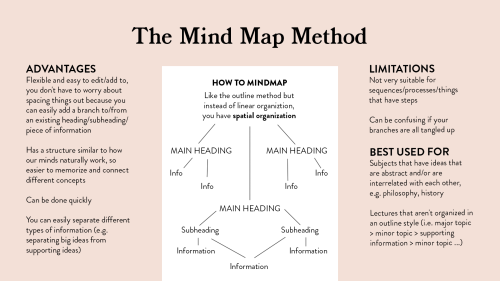
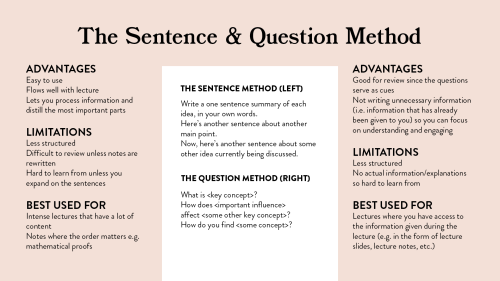
An Overview of Note-Taking Styles

Note-taking is one of the most essential skills a student should master. It allows you to record and review information to be used in the future. But what’s the best way to do so? Here’s an overview of note-taking styles that can help you maximize your learning!

– so what do you do in math?

– algebraic topology, you?

– ugh I always hated algebra. I do probability theory

– ugh I was never any good at probablity theory

Mathematicians be like:

Def 1.1: A function f is fucked-up iff it is not Lebesgue measurable

Def 1.2: A function is evil iff its graph has non-integer Hausdorff dimension.

Exercise 1: Prove that there exist fucked-up and evil functions

1 X 2022

new month huh

yesterday the commutative algebra teacher sent out the first homework assignment. you know, fuck the holiday, we need that grind

I have a week to solve it but I started yesterday as I was so excited

we need to prove some elementary properties of commutative unitary rings and I am enjoying it, I completed a half of the exercises so far. I can tell that the intuition acquired from studying module theory is paying off. many of the requested properties are the special cases of what I encountered during my module venture, so I feel like I understand them quite well. the problem I come across is how to write it down in a rigorous way, but I guess this is why we're supposed to do those exercises

I just got home from the math camp, it was so exhausting. I am not used to being around people all the time, so I my tolerance for interactions is low. I'm glad I went there tho, because I gained some teaching experience – my lecture, choosing contest problems and then grading the solutions

my university offers jobs as graders, older students can make some extra money checking homeworks of younger ones. the requirement is to have a decent GPA, which I don't have so I'm afraid they won't accept me. I don't know how decent exactly tho, so I'm going to try. in particular I might get bonus points for my extracurricular activities, giving talks at conferences and the grading I did at the camp. I'm so done with being poor, I hope I get in. otherwise I might start looking for some programming jobs, not for this academic year but in general, to find out what I could do at all

a few days ago I found a book that I wish I had found sooner: Vector Analysis, Klaus Janich

these are some of the chapters I needed a few months ago for my analysis course. the book is written like a novel and contains many interesting examples. on the bright side there are chapters about riemannian manifolds and other stuff that I haven't yet had an opportunity to study, so I plan to skim through the topics I already know and stay longer at those new to me

well, the sememster starts on tuesday so I don't have much time for that book, but as a sidequest it seems just right