*through Tears* I Don’t Ever Want To Let My Fear Of Failure Trump The Wonder Of Mathematics, I Don’t

I'm reblogging this to compare it later with 1.A from Hatcher's Algebraic Topology. in that chapter he defines the topology on a graph if anyone else wants to check it out

Intuitively, it seems to me that graphs should be some sort of finite topological space. I mean, topology studies "how spaces are connected to themselves", and a graph represents a finite space of points with all the internal connections mapped out. That sounds topological to me! And of course many people consider the Seven Bridges of Königsberg problem to be the "beginning" of topology, and that's a graph theory problem. So graphs should be topological spaces.

Now, I vaguely remember searching for this before and finding out that they aren't, but I decided to investigate for myself. After a bit of thought, it turns out that graphs can't be topological spaces while preserving properties that we would intuitively want. Here's (at least one of the reasons) why:

We want to put some topology on the vertices of our graph such that graph-theoretic properties and topological properties line up—of particular relevance here, we want graph-theoretic connectedness to line up with topological connectedness. But consider the following pair of graphs on four vertices:

On the left is the co-paw graph, and on the right is the cycle graph C_4.

Graph theoretically, the co-paw graph has two connected components, and C_4 has only one. Now consider the subgraph {A, D} of the co-paw graph. Graph theoretically, it is disconnected, and if we want it to also be topologically disconnected, it must by definition be the union of two disjoint open sets. Therefore, in whatever topology we put on this graph, {A} and {D} must be open. The same argument shows that {B} and {C} must be open as well. Therefore the topology on the co-paw graph must be the discrete topology.

Now consider the subgraph {B, D} of C_4. It is disconnected, so again {B} and {D} must be open. Since {A, C} is also disconnected, {A} and {C} must be open. So the topology on C_4 must again be the discrete topology.

But these graphs aren't isomorphic! So they definitely shouldn't have the same topology.

It is therefore impossible to put a topology on the points of a graph such that its graph-theoretic properties line up with its topological properties.

Kind of disappointing TBH.

6 Things People Don't Always Tell You About Studying

1. you ace tests by overlearning. you should know your notes/flashcards/definitions basically by heart. if someone asks you about a topic when you’re away from class or your notes and you can answer them in a thorough and and accurate answer, then you’re good, you know the material. 

2. if you don’t understand something, it will end up on the test. so just don’t disregard and hope that this specific topic won’t be on the test. give it more attention, help, and practice. find a packet of problems on that one concept and don’t stop until you finish it and know it the best. 

3. sometimes you just need that Parental Push. you know in elementary school, they would tell you “ok now it’s time for you to do your homework! you have a project coming up, start looking for a topic now!” ONE of your teachers might be like this. be thankful for it and follow their advice! these teachers are the best at always keeping you on track with their calendar. if not a teacher, then have one of your friends be that person that can keep you accountable for the things you promised you would do. 

4. you just need to kick your own ass. seriously. i know it sucks and its hard to study for two things at once. BUT. I DONT CARE IF IT’S HARD. you need to do it and at least do it to get it over with because you can’t keep putting things off. If you do, you will eventually run out of time and you will hate yourself. force yourself to do it. i made myself sign up for june ACT even though there’s finals because if i didn’t, i probably never would. like do i think i’m gonna be ready in one month? probably not, SO I BETTER GET ON IT AND START STUDYING! 

5. do homework even if it doesn’t count. if you actually try on it, then you will actually do so much better on the tests, it’s like magic. 

6. literally just get so angry about procrastinating that you make yourself start that assignment. I know how hard it is to kick the procrastination habit. I have to procrastinate. So I make myself start by thinking about my deadlines way early. I think, “oh i have a presentation in three weeks (but it really takes 2 weeks to do), i’ll be good and start today.” when that doesn’t happen, you say you’ll do it tomorrow, and this happens for like the next four days. I get so mad at myself for not starting when i am given a new chance to do so with every passing day. By that time, you actually have exactly how much time you need for it AND you were able to procrastinate the same way you usually do ;)

that sounds a bit like mystery flesh pit national park

I’m Christian and respect the order of creation as God intended it but I’m not gonna lie if I could take a massive vat of agar and grow an alive shopping mall made out of red blood and meat and feed it living human bodies to make it expand larger with more shops and amenities, Without hesitation, Without question I would do exactly that

Square is a rhombus, regular hexagon can be tessellated with three equal rhombuses, and every regular polygon with even number of sides can be rhombi-tessellated.

"based and purple pilled" with deleted vowels. the first adhd medication I tried was life changing, I could finally study and function (half-)properly, and the pills are purple, hence my version of "based and red pilled", which I probably don't have to explain

Guys please reply to this with what your url means or references I’m really curious

yes! the same goes for teaching btw. people who just recite the textbook to you are not good teachers. the key to a good explanation of a concept is understanding why someone does not understand it in the first place. and doing that to your own mind when trying to learn something is the point of good learning

also maybe it’s just bc i have a very autistic interest in sociology and human behavior but i like to understand why people think and behave the way they do. it’s been an asset to my ability to advocate for myself and for others. if i know why someone believes something rather than just what they believe, i can have an actual conversation with them. so it always boggles my mind when ppl insist it doesn’t matter why someone believes something, they’re Just Wrong And Should Change Their Mind. like yeah if i could snap my fingers and make someone not transphobic i’d do that but i live on planet earth so the only thing that is gonna potentially get someone to change their mind as long as they’re not too far gone is having an honest conversation with them. i have changed several minds this way, including my own parents, so it’s frustrating to see ppl discouraging this.

ok uh. how do you hypothetically say "i want to study you" in a friendly way

so far the best I've got is "can i join a discord derver that youre in so i can observe you in your natural habitat"

this looks so great! I need to check this out as well

25 VIII 2022

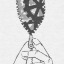
I found the most beautiful math book I have ever seen

it covers the basics of algebraic topology: homotopy, homology, spectral sequences and some other stuff

one of the authors (Fomenko) was a student when this book was being published, he made all the drawings. imagine being an artist and a mathematician aaand making math art

just look at them

other than those drawing masterpieces there are illustrations of mathematical concepts

I'm studying homology right now, so it brings me joy to know that this book exists. I don't know how well it's written yet, but from skimming the first few pages it seems fine

I just finished watching a lecture about exact sequences and I find the concept of homology really pretty: it's like measuring to what extent the sequence of abelian groups fails to be exact

I'm trying to find my way of taking notes. time and again I catch myself zoning out and passively writing down the definitions, so right now I avoid taking notes until it's with a goal of using the writing as a tool for acquiring understanding. I'm trying to create the representations of objects and their basic relations in my mind at first, then maybe use the process of note-taking to further analyze less obvious properties and solving some problems

I will post more about it in the future, we'll see how that goes

When banned from using "trivially" in a proof...

“Hello all. In a fellow mathposter's topology class they were not allowed to use the word "trivially" or any synonym thereof his proofs. The person presenting his work then crossed out "trivially" and wrote instead "indubitably." This inspired him to write a program that will insert condescending adverbial phrases before any statement in a math proof. Trivially, this is a repost. Below is the list--please come up with more if you can!

Obviously

Clearly

Anyone can see that

Trivially

Indubitably

It follows that

Evidently

By basic applications of previously proven lemmas,

The proof is left to the reader that

It goes without saying that

Consequently

By immediate consequence,

Of course

But then again

By symmetry

Without loss of generality,

Anyone with a fifth grade education can see that

I would wager 5 dollars that

By the contrapositive

We need not waste ink in proving that

By Euler

By Fermat

By a simple diagonalization argument,

We all agree that

It would be absurd to deny that

Unquestionably,

Indisputably,

It is plain to see that

It would be embarrassing to miss the fact that

It would be an insult to my time and yours to prove that

Any cretin with half a brain could see that

By Fermat’s Last Theorem,

By the Axiom of Choice,

It is equivalent to the Riemann Hypothesis that

By a simple counting argument,

Simply put,

One’s mind immediately leaps to the conclusion that

By contradiction,

I shudder to think of the poor soul who denies that

It is readily apparent to the casual observer that

With p < 5% we conclude that

It follows from the Zermelo-Fraenkel axioms that

Set theory tells us that

Divine inspiration reveals to us that

Patently,

Needless to say,

By logic

By the Laws of Mathematics

By all means,

With probability 1,

Who could deny that

Assuming the Continuum Hypothesis,

Galois died in order to show us that

There is a marvellous proof (which is too long to write here) that

We proved in class that

Our friends over at Harvard recently discovered that

It is straightforward to show that

By definition,

By a simple assumption,

It is easy to see that

Even you would be able to see that

Everybody knows that

I don’t know why anybody would ask, but

Between you and me,

Unless you accept Gödel’s Incompleteness Theorem,

A reliable source has told me

It is a matter of simple arithmetic to show that

Beyond a shadow of a doubt,

When we view this problem as an undecidable residue class whose elements are universal DAGs, we see that

You and I both know that

And there you have it,

And as easy as ABC,

And then as quick as a wink,

If you’ve been paying attention you’d realize that

By the Pigeonhole Principle

By circular reasoning we see that

When we make the necessary and sufficient assumptions,

It is beyond the scope of this course to prove that

Only idealogues and sycophants would debate whether

It is an unfortunately common misconception to doubt that

By petitio principii, we assert that

We may take for granted that

For legal reasons I am required to disclose that

It is elementary to show that

I don’t remember why, but you’ll have to trust me that

Following the logical steps, we might conclude

We are all but forced to see that

By the same logic,

I’m not even going to bother to prove that

By Kant’s Categorical imperative,

Everyone and their mother can see that

A child could tell you that

It baffles me that you haven’t already realized that

Notice then that

Just this once I will admit to you that

Using the proper mindset one sees that

Remember the basic laws of common sense:

There is a lovely little argument that shows that

Figure 2 (not shown here) makes it clear that

Alas, would that it were not true that

If I’m being honest with you,

According to the pointy-headed theorists sitting in their Ivory Towers in academia,

We will take as an axiom that

Accept for the moment that

These are your words, not mine, but

A little birdie told me that

I heard through the grapevine that

In the realm of constructive mathematics,

It is a theorem from classical analysis that

Life is too short to prove that

A consequence of IUT is that

As practitioners are generally aware,

It is commonly understood that

As the reader is no doubt cognizant,

As an exercise for the reader, show that

All the cool kids know that

It is not difficult to see that

Terry Tao told me in a personal email that

Behold,

Verify that

In particular,

Moreover,

Yea verily

By inspection,

A trivial but tedious calculation shows that

Suppose by way of contradiction that

By a known theorem,

Henceforth

Recall that

Wherefore said He unto them,

It is the will of the Gods that

It transpires that

We find

As must be obvious to the meanest intellect,

It pleases the symmetry of the world that

Accordingly,

If there be any justice in the world,

It is a matter of fact that

It can be shown that

Implicitly, then

Ipso facto

Which leads us to the conclusion that

Which is to say

That is,

The force of deductive logic then drives one to the conclusion that

Whereafter we find

Assuming the reader’s intellect approaches that of the writer, it should be obvious that

Ergo

With God as my witness,

As a great man once told me,

One would be hard-pressed to disprove that

Even an applied mathematician would concede that

One sees in a trice that

You can convince yourself that

Mama always told me

I know it, you know it, everybody knows that

Even the most incompetent T.A. could see,

This won't be on the test, but

Take it from me,

Axiomatically,

Naturally,

A cursory glance reveals that

As luck would have it,

Through the careful use of common sense,

By the standard argument,

I hope I don’t need to explain that

According to prophecy,

Only a fool would deny that

It is almost obvious that

By method of thinking,

Through sheer force of will,

Intuitively,

I’m sure I don’t need to tell you that

You of all people should realize that

The Math Gods demand that

The clever student will notice

An astute reader will have noticed that

It was once revealed to me in a dream that

Even my grandma knows that

Unless something is horribly wrong,

And now we have all we need to show that

If you use math, you can see that

It holds vacuously that

Now check this out:

Barring causality breakdown, clearly

We don't want to deprive the reader of the joy of discovering for themselves why

One of the Bernoullis probably showed that

Somebody once told me

By extrapolation,

Categorically,

If the reader is sufficiently alert, they will notice that

It’s hard not to prove that

The sophisticated reader will realize that

In this context,

It was Lebesque who first asked whether

As is tradition,

According to local folklore,

We hold these truths to be self-evident that

By simple induction,

In case you weren’t paying attention,

A poor student or a particularly clever dog will realize immediately that

Every student brought up in the American education system is told that

Most experts agree that

Sober readers see that

And would you look at that:

And lo!

By abstract nonsense,

I leave the proof to the suspicious reader that

When one stares at the equations they immediately rearrange themselves to show that

This behooves you to state that

Therefore

The heralds shall sing for generations hence that

If I’ve said it once I’ve said it a thousand times,

Our forefathers built this country on the proposition that

My father told me, and his father before that, and his before that, that

As sure as the sun will rise again tomorrow morning,

The burden of proof is on my opponents to disprove that

If you ask me,

I didn’t think I would have to spell this out, but

For all we know,

Promise me you won’t tell mom, but

It would be a disservice to human intelligence to deny that

Proof of the following has been intentially omitted:

here isn’t enough space in the footnote section to prove that

Someone of your status would understand that

It would stand to reason that

Ostensibly,

The hatred of 10,000 years ensures that

There isn’t enough space in the footnote section to prove that

Simple deduction from peano’s axioms shows

By a careful change of basis we see that

Using Conway’s notation we see that

The TL;DR is that

Certainly,

Surely

An early theorem of Gauss shows that

An English major could deduce that

And Jesus said to his Apostles,

This fact may follow obviously from a theorem, but it's not obvious which theorem you're using:

Word on the streets is that

Assuming an arbitrary alignment of planets, astrology tells us

The voices insist that

Someone whispered to me on the subway yesterday that

For surely all cases,

Indeed,

(To be continued)

chaotic good

Pro-tip: You can use paper twice if you take your notes in pencil first and then write over it in pen. 

@shitstudyblr please validate me