I'm Reblogging This To Compare It Later With 1.A From Hatcher's Algebraic Topology. In That Chapter He

ah yes my boy tom cardy. everyone must listen to him, he's the best

I need everyone to see this ABSOLUTE MASTERPIECE

free recall

here I am sitting and trying to learn something from a textbook by making notes and ugh I don't think this is gonna work

what I'm writing down will probably leave my head the second I switch tasks

today I found a cool video about taking notes during lectures and a method called free recall is mentioned there:

to summarize: taking notes during the lecture is ineffective, because it requires dividing attention into writing and processing the auditory input. instead of doing that one should just listen and then try to write down the contents of the lecture from memory. I can believe that – this is how I studied for my commutative algebra exam and the whole process went really fast. I highly recommens this guy's channel, he is a neuroscientist and bases his videos off of research findings

I will try to do this with textbooks and after a while I'll share how it felt and if I plan to keep doing it. the immediate advantage of this approach is that it gives raw information for what needs the most work and what can be skipped, which is often hard to see when trying to evaluate one's knowledge just by thinking about it. another thing that comes to mind is the accountability component – it is much easier to focus on the text while knowing that one is supposed to write down as much as possible after. kinda like the "gamify" trick I saw in the context of surviving boring tasks with adhd

I'll use this method to study differential geometry, algebraic topology, galois theory and statistics. let's see how it goes

I can relate to your undergrad experience! And I think it might be a good sign looking forward, because you've developed insights and ways of thinking and motivation to go beyond undergrad and seek out new spaces where you can do your own work. That's by no means common, I know many fellow undergrads who are a) as mystified when they retake a class as they were the first time round, and b) feel accomplished enough to have passed eg Introductory Analysis and have no drive to look onward. You seem to know very much what you're good at, what interests you and which areas you'd like to grow in. I'd argue that undergrad studies, which give you an introduction and overview of the field and teach basic reasoning skills while not expecting any really original problem solving aren't exactly made for people like you. Talking to your professors or Masters or even PhD students is a really good idea!

thank you for your input, it brings a huge relief!

I already talked to two of my professors and they said that there is nothing to worry about. my advisor said that in his opinion learning new concepts while working on some problem is the right way to learn and from his experience this is way more rewarding than learning for school or even "just to learn". he also said that if I'm interested in working more on open stuff then he will let me know when he finds some questions I could ponder. the other professor said that it's a good thing, because from his experience a lot of people tend to get discouraged when there is no way of knowing how long solving the problem will take or how much new theory is needed, and I seem to be the other way around, so the work I'll be doing in the future probably won't scare me as much

I talked to some of my friends who are about to finish undergrad like me, and there are people who feel the same way as I do. coincidentally, those are the people who had the same situation as mine, that is, they were lucky enough to find an advisor who gave them an open question to work on. other people I talked to seem to be fairly content with studying for the classes and completing homework assignments, and they didn't get to work on something open yet, so maybe it has something to do with getting the taste of the good stuff haha

I can see now that the future looks good and I'm motivated to go exploring. I am aware that I have so much more to learn, but having got the reassurance that I'm probably doing it right, it doesn't sound as scary anymore

did that to me

We need books that affect us like a disaster, that grieve us deeply, like being banished into forests far from everyone. A book must be the axe for the frozen sea within us. That is my belief.

Franz Kafka

that sounds a bit like mystery flesh pit national park

I’m Christian and respect the order of creation as God intended it but I’m not gonna lie if I could take a massive vat of agar and grow an alive shopping mall made out of red blood and meat and feed it living human bodies to make it expand larger with more shops and amenities, Without hesitation, Without question I would do exactly that

25 XII 2022

this chunk of the semester is finally over, sweet jesus I'm so exhausted. I'm getting the well-deserved rest and later catching up with all the things I put on my to-do list that I kinda learned but not really

the test I had last week went fine. frankly I expected more from it after solving more than 50 problems during my prep, but I scored 74%, which is objectively great and more than I predicted after submitting my solutions

here is my math plan for the break:

in algebraic methods I started falling behind a few weeks ago when I missed two lectures while being sick. they were about resolutions, derived functors and group homology and afterwards I wasn't really able to stay on top of my game like before. high time to get back on track. in commutative algebra I was doing ok, but there are some topics I neglected: finite and integral maps and Noether's normalization. for complex analysis everything is great until we introduced the order of growth and recently we've been doing some algebraic number theory, which btw is a huge disappointment. don't get me wrong, I understand the significance of Riemann's ζ, but the problems we did all consisted of subtle inequalities and a lot of technical details. I am doing mainly algebraic stuff to avoid these kind of things lol

when we were doing simplicial sets I stumbled upon some formulas for the simplicial set functor and its geometric realization and I thought it to be a nice exercise to probe them, so here it is:

I won't know if this proof actually works until I attend office hours to find out, but I am satisfied with the work I put into it

I already started making some notes on the derived functors

other than that I have this nice book that will help me prepare for writing my thesis, so I'd like to take a look at that too

as for the non-math plans, I am rewatching good doctor. my brain has this nice property that after a year has passed since finishing a show I no longer remember anything, the exponential distribution is relatable like that. this allows endless recycling of my favourite series, I just need to wait

I wish you all a pleasant break and I hope everyone is getting some rest like I am

Okay I’m currently furious that migraines are often so blindly easy to treat and I had to find this out myself at the age of 26 when I’ve been to a neurologist since I was 11 lol so I’m about to teach you two neat and fast little tricks to deal with pain!

The first is the sternocleidomastoid muscle, or the SCM muscle.

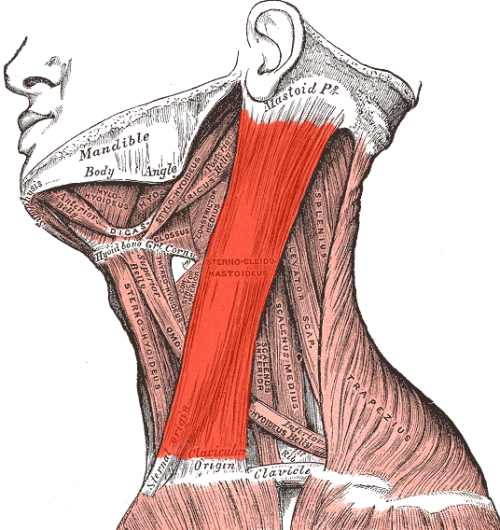
This big red section is responsible for pain around the eye, cheekbone, and jaw, as well as some temple pain. Literally all you have to do is angle your head down a little, angle it away from the side that hurts, and then you can gently pinch and rub that muscle. I find it best to start at the bottom and travel upwards. The relief is so immediate! You can increase pressure as you feel comfortable doing so.

Here is a short and easy video showing this in action

The second is a fast and easy stretch that soothes your vagus nerve, which is the nerve responsible for calming you down. The vagus nerve, for those unfamiliar, is stimulated by deep breathing such as yawning, sighing, singing, or taking a deep breath to calm your anger in a tense situation.

You can stretch this out by sitting up as straight as possible (this does not have to be perfect to work) and interlacing your fingers. Put your hands on the back of your head with your thumbs going down the sides of your neck and, while keeping your face forward, look all the way to one side with just your eyes. Hold that until you feel the urge to breathe deeply or yawn, or until you can tell there’s a change. Then do the same thing on the other side. When you put your arms down, you should clearly be able to turn your head farther in both directions. If the first session doesn’t get rid of your migraine, rest and repeat as many times as necessary. I even get a little fancy with it and roll my eyes up and down along the outer edge sometimes to stretch as much as I can.

If you need a visual here’s a good video on it. I know some of the language they use seems questionable but this is real and simple science and should not be discarded because it’s been adopted by the trendy wellness crowd!

I seriously cannot believe I didn’t hear a word of this from any doctor in my life. Additionally, if you get frequent recurring migraines, you may want to see a dietician. Migraines can be caused by foods containing histamines, lectin, etc. and can also be caused by high blood pressure in specific situations such as exercise, stress, and even sex.

If any of this information helps you I’d love to hear it btw! It’s so so fast and easy to do. Good luck!

when a pelican bites you there's no malice in their eyes. they aren't upset at you. they are just hungry and want to see if you fit in their mouths. and if you don't then it's no problem and everything is fine. and if you do then well i guess your fate is sealed but that's ok it's a beautiful animal

Theory Time

The reason endermen don’t like it when you look at them is because they communicate telepathically with one another by locking eyes! Humans are absolutely not designed to do this so when we look at them we are accidentally projecting all of our thoughts into them at the same time and it hurts :(

30 I 2023

in a fortnight I will have two oral exams and one problem-based exam

the first oral will be for complex analysis and we are supposed to choose three topics from which the professor will pick one and we'll have a chat. I chose meromorphic functions, Weierstrass function and modular function. I have already received my final score from homeworks, which is 73%. combined with 74% and 100% from tests, I am aiming for the top grade

the rest of exams will be for algebraic methods. a friend who already took this course told me that when someone is about to get a passing grade, they get general questions and the professor doesn't demand details of proofs. when I asked him if we are supposed to know the proofs in full detail or if it suffices to just be familiar with the sketch, he told me that if I will only know the sketch I will sit there until I fill in all the details. lmao that sounds like he wants me to get a top grade. ok challenge accepted

so it seems like I have a chance to ace everything. if I achieve this and do it again next semester I can apply for a scholarship. studying for the sole purpose of getting good grades doesn't feel right, the grades should come as a side effect of learning the material. buuut if I can get paid for studying then I might want to try harder, I enjoy being unpoor

the next two weeks will be spent mostly grinding for the algebraic methods exams, this is what I'm doing today