Don't Forget About "you're Gaslighting Me" Whenever You Do Something That They Don't Like. This Is The

BCC

A minimal figure-eight knot on the body-centered cubic lattice

(source code)

Hello, lovelies! I’ve gotten a couple of asks about studying so I decided to condense them into one post for you guys! I’m trying to hit a bunch of different topics so if you need an even more specific post you can send an ask! Without any further ado, have some tips! My studyblr is @spacey-scholar​

Prep

First, you always need a good base for your day! Especially if you’re studying a lot.

Make a good full breakfast! Ex. Eggs and Toast, Smoothie and fruit, Pancakes and a cup of juice. 

How’s your hygiene? Do you need to shower, brush your teeth, wash your face, condition your hair? Do it! You’ll be distracted if you feel messy!

Get dressed like it’s a normal day. Staying in PJ’s is okay! But being ready for the day seriously helps focus!

Likewise, your space should be clean. A clean space is a clean mind! Remove dishes, trash, scrap paper, and extra items. Wide down your desk, organize your pens and books. Your space should feel like your space!

Now make a list of what you need to get done! What needs to be done Now, what needs to be done Soon, and what needs to be done Later? 

Order your list how you want your day to go, and don’t put super-tough subjects back to back, or subjects that are similar exercises i.e. reading thirty pages of two different books back to back is no fun.

The Studying

It’s important to buckle down with No Distractions! If you find yourself distracted put your phone away! If you need your phone, put it on Do Not Disturb until you’re done. I also do this at night for better sleep. 

Pick the best technique for you, Pomodoro, reward-based, group studying, etc.

Play music but only if it will not distract you! If you sing along or daydream it’s the wrong music! Classical, Lo-fi, and White noise are all good! My Spotify Here has some good ones.

Use a nice journal (I don’t mean expensive!) and pens/pencils you enjoy using. I like to have a specific journal and color dedicated to each subject. 

Take notes on recorded lectures and classes, if you’re doing online classes right now try to screen record or record the audio! That way if you space out you can play it later and take notes, and you can absorb the lesson better instead of being distracted.

Don’t worry about your notes, stationary, pictures, being beautiful and your grades being perfect. Life doesn’t always look the way it does on Instagram. And the people who spend hours trying to get a good photo of their coffee are not studying! 

Use flashcards! Quizlet is good if you need premade ones! If you can save up and buy them, Barrons AP Flash Cards are the best in my opinion. Very clean, not too long, very durable, and cover all subjects.

Feeling Distracted 

If you catch yourself drifting off and getting into your head, get up and take a quick walk, stretch, or energizer. 

It’s okay if this happens, don’t guilt yourself! practice affirmation. The best and smartest still get distracted. 

If you are drifting, why? Are you hungry? Tired? Thirsty? Bored? Get a snack and some water, take a break and rest, find a way to make your studying more enjoyable. 

Remember that Motivation and Discipline are different things. Sometimes we just won’t be motivated, we won’t want to do it and it will be rather frustrating. But the cure to this is not shaming its discipline. Remind yourself “This may be hard, and I may not want to do this, but I want to reach my goals and If this is what It takes I will make it happen. 

Always do just one more page of you’re tired. One at a time and oh you did it! Maybe just one more? One more? Eh, one more just to finish the train of thought, Oh just- I’m done? Nice!

If you really can’t focus just move on and come back to this subject, you can always ask for help.

Supplementary Things

There are so many apps you can use to study, for free! My favorites are Tide, Quizlet, Focus Keeper, Forest, Flora, Egenda, SpanishDict, Photomath, and Kahn Academy. 

You can also join a study group! You may know one, but if you don’t, there are a lot of online ones! I’m in a study Discord and have been for a while! it helps a lot and motivates me to finish my work!

You can make a studyblr, but don’t do it just for the aesthetics! It’s about studying, and sometimes that gets messy! Sometimes we fail a test, we spill our tea on our notes, we cry because we don’t understand the formula. That’s the part you don’t see!

Having cute stationery can really help, as well as nice organizers and decorations for your space! I don’t have much money so I get a lot of stuff on Amazon or FB Marketplace.

Health

Remember that no matter what you are good enough. It’s okay if you fail, it’s okay if you struggle.

It’s also okay if your path doesn’t go the way you expected! Maybe you go to a different school than expected! Or choose a trade instead! Maybe you take a gap year! Maybe your passion changes! Maybe it changes six times!

Your health is always more important than your school. If you are in pain, mentally or physically, if you are anxious, exhausted, burnt out, talk to your teachers about it! You matter more than a grade.

Your best is good enough! And your best doesn’t look the same as someone else’s best! Don’t compare!

Now go get out there and study!

Every now and then I remember that Malbolge exists and I get to spend the better part of an hour cry-laughing at the world’s worst programming language

already starting off strong, but it gets worse

Wow! Sounds easy and intuitive to use! What’s the “crazy operation” you ask? We’ll get to that later. For now let’s see what a program in this language looks like :)

Thanks! I hate it!

it’s so difficult to work with that the first program was written by another brute force search program

mmmmm delicious base-3 arithmetic, what could go wrong? (For reference, that means this program forgoes the usual “0/1″ values of binary code in favor of a much more fun “0/1/2″ set of values)

ah.

Here’s how the language actually figures out what to do. It’s got 8 “simple” commands that can be executed easily by *checks notes* running the code itself through the modulo operation and taking the result.

As a bonus, on top of all that every single character in your code will now alter what every single other character does. So I hope you’re alright with cracking a cipher every time you add a new letter to your program!

oh god oh fuck.

behold, Malbolge’s primary arithmetic operation and what you’ll be using for most of your math while programming with it :)

This looks specifically designed to be the least logical math operation you could make, and knowing what the rest of Malbolge is I’d wager that’s precisely what happened. I never want to ever use this and it’s my favorite thing I’ve ever seen.

https://en.wikipedia.org/wiki/Malbolge

Anyways here’s the wiki page if you wanna read through it more deeply, I’m gonna sit here holding in my laughter staring at the hello world program again.

tips for studying math

I thought I could share what I learned about studying math so far. it will be very subjective with no scientific sources, pure personal experience, hence one shouldn't expect all of this to work, I merely hope to give some ideas

1. note taking

some time ago I stopped caring about making my notes pretty and it was a great decision – they are supposed to be useful. moreover, I try to write as little as possible. this way my notes contain only crucial information and I might actually use them later because finding things becomes much easier. there is no point in writing down everything, a lot of the time it suffices to know where to find things in the textbook later. also, I noticed that taking notes doesn't actually help me remember, I use it to process information that I'm reading, and if I write down too many details it becomes very chaotic. when I'm trying to process as much as possible in the spot while reading I'm better at structuring the information. so my suggestion would be to stop caring about the aesthetics and try to write down only what is the most important (such as definitions, statements of theorems, useful facts)

2. active learning

do not write down the proof as is, instead write down general steps and then try to fill in the details. it would be perfect to prove everything from scratch, but that's rarely realistic, especially when the exam is in a few days. breaking the proof down into steps and describing the general idea of each step naturally raises questions such as "why is this part important, what is the goal of this calculation, how to describe this reasoning in one sentence, what are we actually doing here". sometimes it's possible to give the proof purely in words, that's also a good idea. it's also much more engaging and creative than passively writing things down. another thing that makes learning more active is trying to come up with examples for the definitions

3. exercises

many textbooks give exercises between definitions and theorem, doing them right away is generally a good idea, that's another way to make studying more active. I also like to take a look at the exercises at the end of the chapter (if that's the case) once in a while to see which ones I could do with what I already learned and try to do them. sometimes it's really hard to solve problems freshly after studying the theory and that's what worked out examples are for, it helps. mamy textbooks offer solutions of exercises, I like to compare the "official" ones with mine. it's obviously better than reading the solution before solving the problem on my own, but when I'm stuck for a long time I check if my idea for the solution at least makes sense. if it's similar to the solution from the book then I know I should just keep going

4. textbooks and other sources

finding the right book is so important. I don't even want to think about all the time I wasted trying to work with a book that just wasn't it. when I need a textbook for something I google "best textbooks for [topic]" and usually there is already a discussion on MSE where people recommend sources and explain why they think that source is a good one, which also gives the idea of how it's written and what to expect. a lot of professors share their lecture/class notes online, which contain user-friendly explenations, examples, exercises chosen by experienced teachers to do in their class, sometimes you can even find exercises with solutions. using the internet is such an important skill

5. studying for exams

do not study the material in a linear order, instead do it by layers. skim everything to get the general idea of which topics need the most work, which can be skipped, then study by priority. other than that it's usually better to know the sketch of every proof than to know a half of them in great detail and the rest not at all. it's similar when it comes to practice problems, do not spend half of your time on easy stuff that could easily be skipped, it's better to practice a bit of everything than to be an expert in half of the topics and unable to solve easy problems from the rest. if the past papers are available they can be a good tool to take a "mock exam" after studying for some time, it gives an opoortunity to see, again, which topics need the most work

6. examples and counterexamples

there are those theorems with statements that take up half of the page because there are just so many assumptions. finding counterexamples for each assumption usually helps with that. when I have a lot of definitions to learn, thinking of examples for them makes everything more specific therefore easier to remember

7. motivation

and by that I mean motivation of concepts. learning something new is much easier if it's motivated with an interesting example, a question, or application. it's easier to learn something when I know that it will be useful later, it's worth it to try to make things more interesting

8. studying for exams vs studying longterm

oftentimes it is the case that the exam itself requires learning some specific types of problems, which do not really matter in the long run. of course, preparing for exams is important, but keep in mind that what really matters is learning things that will be useful in the future especially when they are relevant to the field of choice. just because "this will not be on the test" doesn't always mean it can be skipped

ok I think that's all I have for now. I hope someone will find these helpful and feel free to share yours

19 I 2023

this week is kinda crazy

I have a complex analysis test on saturday and the professor said that it will cover the entire semester. thank god I might get away with not knowing anything about analytic number theory lmao

I had troubles sleeping lately, it takes me about 3-4 hours to fall asleep every day. I sleep a lot during the day and it helps a bit but I still feel half-dead all the time. every time I fall asleep my brain can't shut up about some math problem

for the algebraic methods course we were supposed to state and prove the analogue of Baer criterion for sheaves of rings. I was the only person who claimed to have solved this, so I was sentenced to presenting my solution in front of everyone. the assertion holds and I thought I proved it but the professor said that the proof doesn't work, here is what I got:

he said that we cannot do this on stalks and we have to define a sheaf of ideals instead. when I was showing this I had a migraine so no brain power for me, I couldn't argue why I believe this to be fine. whenever two maps of sheaves agree on each stalk they are equal, so if we show that every extension on stalks is actually B → M on stalks, then doesn't that imply the extension is B → M on sheaves?? probably not, but I don't see where it fails and I'm so pissed that I was unable to ask about it when I was presenting, now it's too late and this shit keeps me up at night

I enjoy sheaf theory very much and I can't wait to have some time to read about schemes, I have a feeling that algebraic geometry and I are gonna be besties

during some interview Eisenbud said that when deciding which speciality to choose one should find a professor that they like and just do what that professor is doing lol. I feel this now that I talked some more to the guy who taught us commutative algebra. since my first year I was sure that I will do algebraic topology but maybe I will actually do AG, because that's what he's doing. is having one brain enough to do both?

anyway I'm glad that my interests fall into the category of fashionable stuff to do in math these days. my bachelor's thesis is likely going to be about simply-connected 4-dimensional manifolds, which is a hot research topic I guess. I won't work on any open problem because I'm just a stupid 3-year, not Perelman, but it will be a good opportunity to learn some of the stuff necessary to do research one day

imo euclidean geometry kinda sucks, but if we mean geometry in a more general sense then algebraic geometry is the one

I've decided to start a fight

anyways geometry sucks algebra best math

25 VIII 2022

I found the most beautiful math book I have ever seen

it covers the basics of algebraic topology: homotopy, homology, spectral sequences and some other stuff

one of the authors (Fomenko) was a student when this book was being published, he made all the drawings. imagine being an artist and a mathematician aaand making math art

just look at them

other than those drawing masterpieces there are illustrations of mathematical concepts

I'm studying homology right now, so it brings me joy to know that this book exists. I don't know how well it's written yet, but from skimming the first few pages it seems fine

I just finished watching a lecture about exact sequences and I find the concept of homology really pretty: it's like measuring to what extent the sequence of abelian groups fails to be exact

I'm trying to find my way of taking notes. time and again I catch myself zoning out and passively writing down the definitions, so right now I avoid taking notes until it's with a goal of using the writing as a tool for acquiring understanding. I'm trying to create the representations of objects and their basic relations in my mind at first, then maybe use the process of note-taking to further analyze less obvious properties and solving some problems

I will post more about it in the future, we'll see how that goes

I've been thinking about how different math feels after three years of consistently doing it. it's a sad thought, because I used to get super excited about learning new things and solving problems, whereas now my standards seem to be higher..?

I spent the day doing exercises from galois theory and statistics, in preparation for the tests I have soon. it felt like a chore. sure, the exercises were easy and uninteresting, I decided to start from the basics, so there is that. however, in general practicing like this became a routine and there used to be a sense of mystery around it that is now gone

when I don't have any deadlines but feel like doing some math the obvious choice is to learn something that will be useful in the future. more homological algebra, algebraic geometry, K-theory, or digging deeper into the topics I already am familiar with. all of those are good candidates and I used to be very motivated to just learn something new. but here comes to paradox of choice, where every option is good, but there isn't a great one

I think I might be annoyed with always learning the prerequisites for something not yet defined. it did feel exciting when I was studying the modules of tangles so that I could answer an open question, it doesn't feel as exciting to learn about the galois theory to pass a test. a metaphor comes to mind. doing math without a fulfilling goal feels like taking a walk – it's rather nice, I enjoy going on walks. with a fulfilling goal it feels like walking towards a destination such that the walk itself is a pleasant activity, but I really want to get to said destination. by that I mean that I still enjoy simply learning new stuff and working on exercises, but it doesn't feel as fulfilling as it used to, how much walking without getting anywhere can you do in three years? you can do the same thing in prison

three years is nothing compared to how much knowledge and experience is necessary to do actual research, I know that. I fail to feel it, but I know it. when I am asking myself what state of mind is the most fulfilling I'd say exploration, discovery, getting an idea that is new to me and seemingly comes from nowhere, not just an obvious corollary of what I've seen in lectures, an insight, an act of creating. I suppose all those things are to be found in the future, but god how long do I have to wait

on a more pragmatic and realistic note, I think I'll talk to my professors about what I can do to speed up that process. I'll ask them how the actual research feels and how they went from being a student learning basic concepts to where they are now

a question to those of you who are more experienced than me: does this even sound familiar at all? what were you like as a student and what took you to where you are now? how does math feel after 3, 5, 10 years?

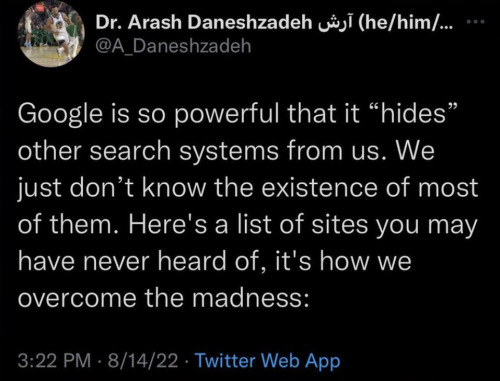
refseek.com

www.worldcat.org/

link.springer.com

http://bioline.org.br/

repec.org

science.gov

pdfdrive.com

thinking about the time a prof told us that in real research mathematics it's fine to be slow, speed itself is not essential, as long as you can find it within yourself to make consistent unyielding inexorable forward progress, like the time some guy stole an M60A3 tank and terrorized a suburban neighborhood with it, said guy wasn't going that fast but plowed through cars and telephone poles and shit no problem. i'm not kidding that's what he said, that's the metaphor he used, he told us that the act of mathematics is like the 1995 san diego tank rampage