25 VIII 2022

Hello, lovelies! I’ve gotten a couple of asks about studying so I decided to condense them into one post for you guys! I’m trying to hit a bunch of different topics so if you need an even more specific post you can send an ask! Without any further ado, have some tips! My studyblr is @spacey-scholar​

Prep

First, you always need a good base for your day! Especially if you’re studying a lot.

Make a good full breakfast! Ex. Eggs and Toast, Smoothie and fruit, Pancakes and a cup of juice. 

How’s your hygiene? Do you need to shower, brush your teeth, wash your face, condition your hair? Do it! You’ll be distracted if you feel messy!

Get dressed like it’s a normal day. Staying in PJ’s is okay! But being ready for the day seriously helps focus!

Likewise, your space should be clean. A clean space is a clean mind! Remove dishes, trash, scrap paper, and extra items. Wide down your desk, organize your pens and books. Your space should feel like your space!

Now make a list of what you need to get done! What needs to be done Now, what needs to be done Soon, and what needs to be done Later? 

Order your list how you want your day to go, and don’t put super-tough subjects back to back, or subjects that are similar exercises i.e. reading thirty pages of two different books back to back is no fun.

The Studying

It’s important to buckle down with No Distractions! If you find yourself distracted put your phone away! If you need your phone, put it on Do Not Disturb until you’re done. I also do this at night for better sleep. 

Pick the best technique for you, Pomodoro, reward-based, group studying, etc.

Play music but only if it will not distract you! If you sing along or daydream it’s the wrong music! Classical, Lo-fi, and White noise are all good! My Spotify Here has some good ones.

Use a nice journal (I don’t mean expensive!) and pens/pencils you enjoy using. I like to have a specific journal and color dedicated to each subject. 

Take notes on recorded lectures and classes, if you’re doing online classes right now try to screen record or record the audio! That way if you space out you can play it later and take notes, and you can absorb the lesson better instead of being distracted.

Don’t worry about your notes, stationary, pictures, being beautiful and your grades being perfect. Life doesn’t always look the way it does on Instagram. And the people who spend hours trying to get a good photo of their coffee are not studying! 

Use flashcards! Quizlet is good if you need premade ones! If you can save up and buy them, Barrons AP Flash Cards are the best in my opinion. Very clean, not too long, very durable, and cover all subjects.

Feeling Distracted 

If you catch yourself drifting off and getting into your head, get up and take a quick walk, stretch, or energizer. 

It’s okay if this happens, don’t guilt yourself! practice affirmation. The best and smartest still get distracted. 

If you are drifting, why? Are you hungry? Tired? Thirsty? Bored? Get a snack and some water, take a break and rest, find a way to make your studying more enjoyable. 

Remember that Motivation and Discipline are different things. Sometimes we just won’t be motivated, we won’t want to do it and it will be rather frustrating. But the cure to this is not shaming its discipline. Remind yourself “This may be hard, and I may not want to do this, but I want to reach my goals and If this is what It takes I will make it happen. 

Always do just one more page of you’re tired. One at a time and oh you did it! Maybe just one more? One more? Eh, one more just to finish the train of thought, Oh just- I’m done? Nice!

If you really can’t focus just move on and come back to this subject, you can always ask for help.

Supplementary Things

There are so many apps you can use to study, for free! My favorites are Tide, Quizlet, Focus Keeper, Forest, Flora, Egenda, SpanishDict, Photomath, and Kahn Academy. 

You can also join a study group! You may know one, but if you don’t, there are a lot of online ones! I’m in a study Discord and have been for a while! it helps a lot and motivates me to finish my work!

You can make a studyblr, but don’t do it just for the aesthetics! It’s about studying, and sometimes that gets messy! Sometimes we fail a test, we spill our tea on our notes, we cry because we don’t understand the formula. That’s the part you don’t see!

Having cute stationery can really help, as well as nice organizers and decorations for your space! I don’t have much money so I get a lot of stuff on Amazon or FB Marketplace.

Health

Remember that no matter what you are good enough. It’s okay if you fail, it’s okay if you struggle.

It’s also okay if your path doesn’t go the way you expected! Maybe you go to a different school than expected! Or choose a trade instead! Maybe you take a gap year! Maybe your passion changes! Maybe it changes six times!

Your health is always more important than your school. If you are in pain, mentally or physically, if you are anxious, exhausted, burnt out, talk to your teachers about it! You matter more than a grade.

Your best is good enough! And your best doesn’t look the same as someone else’s best! Don’t compare!

Now go get out there and study!

30 VIII 2023

aight it's been a while, time for an update

recently I've been doing mostly algebraic geometry, my advisor gave me some stuff to read, so I'm working through that. the goal is to familiarize myself with hilbert schemes – the topic is advanced, so there are many prerequisites coming up when I'm trying to read the book, that's kinda annoying

we are planning for my thesis to be about a certain generalization of the hilbert scheme, so basically the question is "investigate this space" and I've been having second thoughts whether I'm up for the challenge. I'm just getting to know how all that stuff works, so it's quite overwhelming to see how much I need to learn before I can do anything on my own

nevertheless, I'm pushing through as I will have to learn all of that anyway

I am working on finishing the proof from my bsc thesis and honestly I'm kinda losing hope lmao it turns out that what I probably have to do to complete it is a massive amount of extra reading and an even bigger amount of proving lemmas. the thing is that my work is about something like a generalization of results that have been proven by two people (one of which is khovanov, yes, that khovanov) and I feel it in my balls that the case I'm working on should be treated in a similar way. now the problem is that I can barely understand what they wrote for the "easier" case and I just can't see myself doing that for the more complicated one. oh and for my case I should probably use equivariant cohomology. but all I know about it is the definition, I have never even calculated anything for that + I will do a course on it this semester so it feels futile to study it now. idk I need to talk to my former advisor about this and ask him to be honest, does he even believe that this can be done?

other than that I'm applying for a scholarship. I don't think I will get it, but it is worth trying

I moved in with my boyfriend and our cat decided that my desk is way too big for one person, so now it's our desk

uni starts in a month so I should probably spend that time doing something other than math, which I will be doing all the time once uni starts, but I struggle with coming up with things to do that are not math-related. I should complete some tasks for work, but I would also like to have a hobby

there is a number of things that I could try, for instance reading, drawing, singing, grinding metas for geoguessr (apparently I'm a gamer now), but I can't commit to any of those, my interest comes in waves

maybe I could schedule about an hour per day to do one of those things so that my brain gets used to it. it is not like I can focus on math 24/7, I need to take breaks and I have days when my motivation is zero, so I just sit at my desk and watch stupid shit on youtube. but that's the point, days like that could be spent doing something meaningful and refreshing, instead I just procrastinate math lol

So the exponential function is given by

which evaluated at a real number x gives you the value eˣ, hence the name. There are various ways of extending the above definition, such as to complex numbers, or matrices, or really any structure in which you have multiplication, summation, and division by the values of the factorial function at whatever your standin for the natural numbers is.

For a set A we can do some of these quite naturally. The product of two sets is their Cartesian product, the sum of two sets is their disjoint union. Division and factorial get a little tricky, but in this case they happen to coexist naturally. Given a natural number n, a set that has n! elements may be given by Sym(n), the symmetric group on n points. This is the set of all permutations of {1,...,n}, i.e. invertible functions from {1,...,n} to itself. How do we divide Aⁿ, the set of all n-tuples of elements of A, by Sym(n) in a natural way?

Often when a division-like thing with sets is written like A/E, it is the case that E is an equivalence relation on A. The set of equivalence classes of A under E is then denoted A/E, and called the quotient set of A by E. Another common occurence is when G is a group that acts on A. In this case A/G denotes the set of orbits of elements of A under G. This is a special case of the earlier one, where the equivalence relation is given by 'having the same orbit'. It just so happens that the group Sym(n) acts on naturally on any Aⁿ.

An element of Aⁿ looks like (a[1],a[2],...,a[n]), and a permutation σ: {1,...,n} -> {1,...,n} acts on this tuple by mapping it onto (a[σ(1)],a[σ(2)],...,a[σ(n)]). That is, it changes the order of the entries according to σ. An orbit of such a tuple under the action of Sym(n) is therefore the set of all tuples that have the same elements with multiplicity. We can identify this with the multiset of those elements.

We find that Aⁿ/Sym(n) is the set of all multisubsets of A with exactly n elements with multiplicity. So,

is the set of all finite multisubsets of A. Interestingly, some of the identities that the exponential function satisfies in other contexts still hold. For example, exp ∅ is the set of all finite multisubsets of ∅, so it's {∅}. This is because ∅⁰ has an element, but ∅ⁿ does not for any n > 0. In other words, exp 0 = 1 for sets. Additionally, consider exp(A ⊕ B). Any finite multisubset of A ⊕ B can be uniquely identified with an ordered pair consisting of a multisubset of A and a multisubset of B. So, exp(A + B) = exp(A) ⨯ exp(B) holds as well.

For A = {∗} being any one point set, the set Aⁿ will always have one element: the n-tuple (∗,...,∗). Sym(n) acts trivially on this, so exp({∗}) = {∅} ⊕ {{∗}} ⊕ {{∗∗}} ⊕ {{∗∗∗}} ⊕ ... may be naturally identified with the set of natural numbers. This is the set equivalent of the real number e.

5x5 Diamond rule, iterates 1-32

Iterates 40, 48, 56

Iterate 64

Iterate 128

This is a 2D cellular automaton generating a 3D fractal layer by layer. I coded it in Microsoft Excel - each pixel is 1 cell.

See more MSExcel fractals

for the sake of an updates to this, I didn't get 100% on that topology test. I got 85%, which was the third best score. I finally scored the highest possible final grade on that subject, so I'm satisfied. fuck I love algebraic topology so much and I think she loves me

oh and I scored fucking 54% on the analysis test. I think I had a mental orgasm when I found out about that lmao it felt so good. I finished the course with a grade of 4 (idk if it's universal, so 2=the lowest, failed, 5=the highest) which is the best I ever got in the analysis course

28 V 2022

topology and analysis tests are over, both went I think alright

if I don't get 100% from topo I'm going to be very frustrated, because I studied hard and acquired deep understanding of the material – so far as to be able to hold a lecture for my classmate about any topic

analysis ughhh if I get ≥40% I will be overjoyed. but that's just the specifics of this subject, you study super hard and seem to be entirely ready, you solve all of the problems in prep and then best you can do is 40%. my best score so far was 42%, so anything more than that will be my lifetime record lmao, I want this so bad. I solved two problems entirely I think, which should give 40% already, and some pieces from two more, chances are I get 50%, which would be absolutely amazing

here are some pictures from me transforming math into an art project

stokes theorem

topology

I was thinking about how annoying I find what people say to me when I tell them that I'm not happy with how I'm doing at math. their first idea is to tell me how great I am and how all I do is good enough and shit like that. it doesn't help, it just feels like I am not being taken seriously. when I barely pass anything, am I really supposed to believe that everything is actually good? it feels like they skip getting to know my situation and just tell me what they would tell anyone, automatic

when I try to calm myself down and think something that will keep me going I don't try to force myself to be happy, fuck that, not being content with one's achievements is very fine, I believe not being happy all the time is fully natural and all that positivity feels so fake

instead what seems to work is asking myself where the rational threshold of being ok with how I'm doing is. the thing is I will never be satisfied, whatever I have, I always want more. but I can set the limits in advance and that stops me from falling into self-loathing loops

although what has really changed the game for me was getting a few good grades, finally I am achieving something, anything. people tell me that I should learn to be alright without this external reliance on achievements but how am I supposed to do that when the source of my low moods is precisely getting less than I want? I don't understand why I should brainwash myself into thinking that this is actually not what I want. the trick here is to separate the goal-orientedness from the sense of self-worth. the groundbreaking realization of mine was figuring out that I believe I deserve more than I get, that's why I am unhappy. so now that I am getting what I think what I deserve I obviously feel much better

BCC

A minimal figure-eight knot on the body-centered cubic lattice

(source code)

21 I 2023

so the test I had today, our professor went crazy with grading it and we all had our scores by midnight

I don't think I ever scored 100% before, but here it is

I was insanely lucky. yesterday I was watching some series (and by that I mean Young Royals, not Fourier) and I had a thought you know might as well give them elliptic functions a quick read. today one of the easy problems required to only know the basic definitions and properties, have I not spent those 40 minutes reading I would probably not solve it. the other easy problem was solved by picard's theorems, my favourite, which I tried to use with every given opportunity so now it's as they say: when your only tool is a hammer every problem looks like a nail. and today it actually was a nail. two other problems were just objectively easy and the last one took a lot of my time but it was "my type" of problems, so I enjoyed working on it and I had some good ideas thanks to solving about 20 similar problems before

so that's how it feels to reach above my goals. I dreamt of this moment and it feels exactly like I thought it would. ah feels good man

moreover tiktok adhd content is not even good lol most of it is videos themed "things I didn't know were adhd" and they actually are personality traits and it's not helpful at all with anything

just saw a post complaining about how hard it is to find adhd resources for adults and one of the comments said “tiktok has a lot of adhd tips” as if telling someone with adhd to enter the algorithmic quicksand of perpetual dopamine hits isn’t the most insane thing you could suggest for someone with adhd

abstract algebra things that are good:

groups. i love taking inverses

fields. i LOVE taking inverse

banach algebras. i love having a notion of distance, and also being a complete space

lie groups. i dont know anything about them yet. but they seem so cool. technically groups

abstact algebra things that are bad:

rings. god i hate rings so much. theres like a thousand different kinds of rings, some of which are subsets of each other, and some of which have different names but are actually the same.

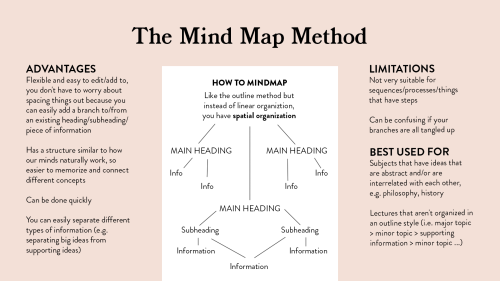
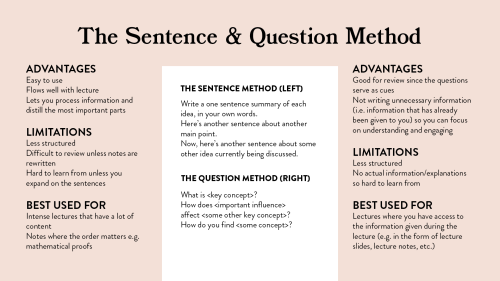
An Overview of Note-Taking Styles

Note-taking is one of the most essential skills a student should master. It allows you to record and review information to be used in the future. But what’s the best way to do so? Here’s an overview of note-taking styles that can help you maximize your learning!