Types Of Mathematical Terminology

reverse gaslighting where i pretend to know exactly what you are talking about

in a way. over the last two years or so. mathematics has become the altar at which I pour out my private grief, and transmute it to something like solace. it does not particularly matter to me if I am ever any good at it. what matters is that the effort I apply to it is rewarded by understanding. I have no natural aptitude for it; I am climbing this hill because it was the steepest and least hospitable to me. there is less agony in the gentler slope, but less valor

everybody cries doing their math hw, those who claim they don't just haven't met that hw yet

this unlocked some ancient pain lol

I am so fucking normal right now. *stands perpendicular to the tangent of the plane*

Weaving Stereographic Projection

I made a stereographic projection by weaving paper strips!

Here's a Julia package for the computation of the shapes of the paper strips.

GitHub

GitHub - hyrodium/ElasticSurfaceEmbedding.jl: The weaving paper strips: shape optimization by geometric elasticity

The weaving paper strips: shape optimization by geometric elasticity - GitHub - hyrodium/ElasticSurfaceEmbedding.jl: The weaving paper strip

Japanese blog post about this: https://note.com/hyrodium/n/n7b7cf03a7d91

25 XII 2022

this chunk of the semester is finally over, sweet jesus I'm so exhausted. I'm getting the well-deserved rest and later catching up with all the things I put on my to-do list that I kinda learned but not really

the test I had last week went fine. frankly I expected more from it after solving more than 50 problems during my prep, but I scored 74%, which is objectively great and more than I predicted after submitting my solutions

here is my math plan for the break:

in algebraic methods I started falling behind a few weeks ago when I missed two lectures while being sick. they were about resolutions, derived functors and group homology and afterwards I wasn't really able to stay on top of my game like before. high time to get back on track. in commutative algebra I was doing ok, but there are some topics I neglected: finite and integral maps and Noether's normalization. for complex analysis everything is great until we introduced the order of growth and recently we've been doing some algebraic number theory, which btw is a huge disappointment. don't get me wrong, I understand the significance of Riemann's ζ, but the problems we did all consisted of subtle inequalities and a lot of technical details. I am doing mainly algebraic stuff to avoid these kind of things lol

when we were doing simplicial sets I stumbled upon some formulas for the simplicial set functor and its geometric realization and I thought it to be a nice exercise to probe them, so here it is:

I won't know if this proof actually works until I attend office hours to find out, but I am satisfied with the work I put into it

I already started making some notes on the derived functors

other than that I have this nice book that will help me prepare for writing my thesis, so I'd like to take a look at that too

as for the non-math plans, I am rewatching good doctor. my brain has this nice property that after a year has passed since finishing a show I no longer remember anything, the exponential distribution is relatable like that. this allows endless recycling of my favourite series, I just need to wait

I wish you all a pleasant break and I hope everyone is getting some rest like I am

7 III 2023

it's the second week of the semester and I must say that it's easier than I predicted

statistical data analysis is boring but easy, algebra 2 is easy but probably interesting, so is differential geometry

algebraic topology was funny because ⅓ of the group completed the algebraic methods course, so at first we told the professor to skip half of the lecture (we all know the required part of category theory) and then with every new piece of information he would say "ok maybe this will be the first thing today that you don't know", to which we would reply "naaah we've seen this" lmao. but the course overall will be fun and maybe it's even better that the level of difficulty won't be as high as I though, that would leave more time for my other stuff

the tutorial part of number theory was scary, because the professor wanted us to work in pairs. my autistic ass hates working in groups and the noise in the room was unbearable (everyone was talking about the exercises we were given to solve), so I was on the verge of a meltdown after 30 minutes of this despite ANC headphones. next time I will work by myself from the start. maybe without the requirement of communication it won't be as bad. the course itself will be easy, when it comes to the material. I know nothing about number theory, so the novelty will make it more enjoyable. a few people said that they would prefer the tutorial in the standard form, maybe I won't have to worry about surviving it if there are enough people who want to change it

my birthday is tomorrow and as a gift my parents gave me enough money to buy an ipad, I was saving for it since november. for a few days now I've been testing different apps for note taking, pdf readers and other tools useful for studying. I must say, this is a game changer, I absolutely love it

taking notes itself is less comfortable than on an e-ink tablet, which gives very paperlike experience, but it's better than traditional ones. the upside is that I can use different colors and the whole process is less rigid than on an e-ink

two apps that seem the best for now are MarginNote 3 and GoodNotes

the first one is good for studying something from multiple sources. the app allows to open many pdfs, take pieces from them and then arrange them in a mindmap. it's possible to add handwritten notes, typed notes, photos and probably more that I don't know yet. all of this seems to be particularly useful when studying for exams or in other situations when it's necessary to review a huge chunk of material

the second app is for regular handwritten notes. it doesn't have any special advantages other than I just like the interface lol what I like about taking notes on ipad is that I can take photos and insert them directly into the notebook, which I can't do on the e-ink. it's great for lectures and classes because I don't usually write everything down (otherwise I can't listen, too busy with writing) and even if I do, I don't trust myself with it so I take photos anyway. being able to merge the photos with notes reduces chaos

oh god this is going to be a long post! other news from life is that yesterday I had a meeting with my thesis advisor and we finally picked a topic. some time ago he sent me a paper to try and said, very mysteriously, to let him know if it's not too hard before he reveals more details about his idea. the paper is about symmetric bilinear forms on finite abelian groups, pure algebra, and I was supposed to write about algebraic topology, so I tried to search where this topics comes up, but didn't find anything. it turns out that it's used to define some knot invariant, which I would use to write about the classification of singularities of algebraic curves. in the meantime my advisor had another idea, which is an open problem in knot theory. we decided to try the second one, because there is less theory to learn before I could start writing the paper

to summarize what I'm about to do: there is a knot invariant called Jones polynomial, which then inspires a construction of a certain R-module on tangles and the question asks whether that module is free, if so, what is its rank. now I'm reading the book he gave me to learn the basics and I can't wait till I start working on the problem

yes, this, but also among other stem courses in a typical school, math is taken the most seriously. idk about other countries, but in poland in highschool people study chemistry, biology, physics and geography only if they decide to take the advanced final exams in these subjects. with math, everyone has take the standard level exam, so it can't be ignored like other subjects

up to highschool everyone has to complete their share of stem courses, but with the subjects other than math, the teachers often allow students to pass by memorizing the theory or by making some extra projects to earn points. with math you can't do that. when someone struggles with physics, the teacher sometimes says "alright, next year you won't have to study physics, so just learn those formulas and definitions and write them down on a test and I will let you pass". in math this is not an option, the student will have to take n more years of math courses

also, math mainly requires learning new skills, not just new information. many people never memorize the "dry theory" in highschool, because you have access to a reference table of formulas during exams and your job is only to know where to use those formulas – no need to memorize anything. but this does not come naturally to everyone and I think a huge part of the problem is teaching people how to work on their problem solving skills. I tutored a few students who believed they were bad at math and their mindset was "I can solve this type of problem because I know how to substitute into this formula, but when the problem is slightly different I panic, because the teacher never showed us how to solve it", which can be fixed by practicing a wider variety of problems and practicing the awareness of one's thinking process

people do not understand that problem solving is a skill on its own and I blame schools for that, because what we are offered is the image of math being about re-using the same kind of thinking processes but with different numbers. heck, when I was in elementary school I thought this is what math is about and I hated it because it's so boring and repetitive. I can imagine, when someone believes that this is what math is supposed to be and then they see the "more real math", which is about creativity, they panic (and rightfully so, they've been lied to)

my unpopular opinion is that not everyone can be good at this, just like I will never be good at understanding literature – my brain just sucks at processing this kind of stuff and I have aphantasia which doesn't help at all. but what makes it even worse for those people is the belief that it should be about repeating the same patterns over and over, so when they see that it's something completely different, it must be very frustrating – the reality is inconsistent with their beliefs

I am sure it doesn't cover the entirety of the "oof I always hated math" phenomenon, but it certainly does explain some of it, especially in the context of the education system in my country

As I said in a previous post, I have deep sympathy for the frustration of people who are good at math when they see math so almost universally hated by children and adults

And again and again, they try to explain that math is very much within everyone's reach and can be fun and, at least in western countries, education was to blame, messing up this very doable and fun thing by teaching it wrong

But I still gotta wonder - why math? If it is really just education messing this up, why does it mess up so much with math, specifically? I'm sorry but I still cannot shake the sense that even if it's just bad teaching, math is especially vulnerable to bad teaching.

Or is it maybe just that math is the only truly exact science, so there is no margin of error, so unlike every other field where you can sortof weasel around and get away with teaching and retaining half-truths and oversimplifications and purely personal opinions, math is unforgiving with the vague and the incorrect?

ok now i might have some kind of super memory??

a week ago i played chess with bf and we didn't finish, so now i arranged the board as i remembered it and i got 13 out of 14 pieces correctly

i mean wow i didn't know i am capable of something like this

might be autism i suspect i might have

anyway now i want to know everything about human memory and take advantage of that

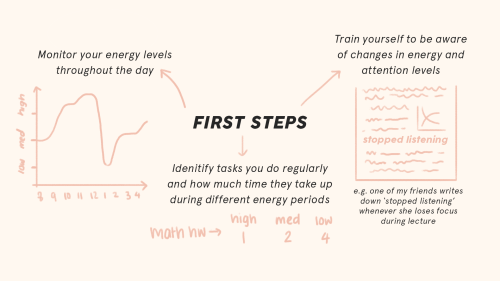
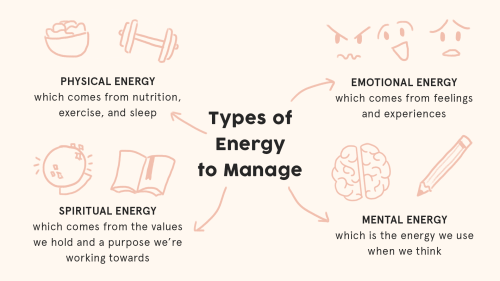
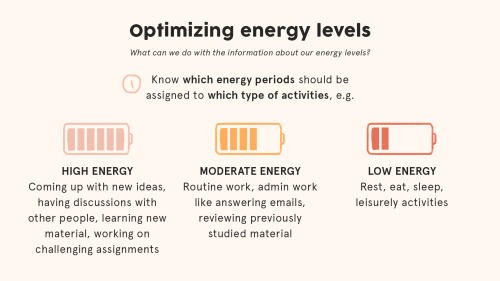
Energy Management

A human-based organization method

click on images for better resolution; images also available here (link to google drive)

Other posts that may be of interest:

Getting stuff done: How to deal with a lack of motivation

Flexible time-blocking: A more breathable way to get things done

The ABCDE Method