Cool !

Scutoid

The newly discovered shape that shows how nature packs cells efficiently into three-dimensional structures.

Researchers have discovered a new geometric shape that’s been hiding in plain sight.

A team studying the cells that give rise to embryos and can be found lining our organs and blood vessels pinpointed a three-dimensional shape that occurs as they bend and pack together.

The new shape, dubbed the scutoid, allows these epithelial cells to organize with the most efficiency, as opposed to the column or bottle-like shapes scientists previously attributed to this process.

Treating a human head the way a globe is treated by the Mercator projection.

INTERNATIONAL KWEEN OF TRIGONOMETRY

Uma cidade perfeita para os exercícios de matemática!

Satellite map of Missoula, Montana

The regular hexagon hidden in a cube unfolds to a straight line on a net of the cube.

MATH SYMBOLS

If one remembers this particular episode from the popular sitcom ‘Friends’ where Ross is trying to carry a sofa to his apartment, it seems that moving a sofa up the stairs is ridiculously hard.

But life shouldn’t be that hard now should it?

The mathematician Leo Moser posed in 1966 the following curious mathematical problem: what is the shape of largest area in the plane that can be moved around a right-angled corner in a two-dimensional hallway of width 1? This question became known as the moving sofa problem, and is still unsolved fifty years after it was first asked.

The most common shape to move around a tight right angled corner is a square.

And another common shape that would satisfy this criterion is a semi-circle.

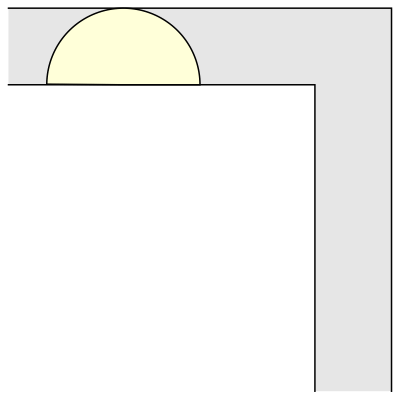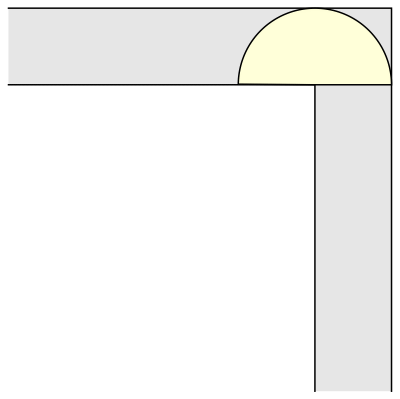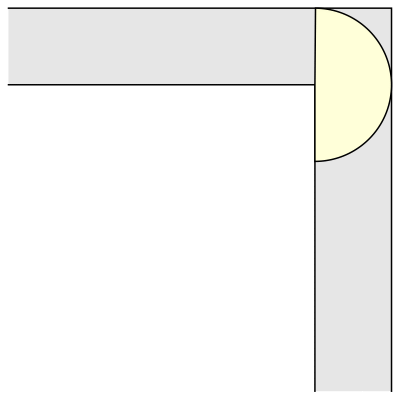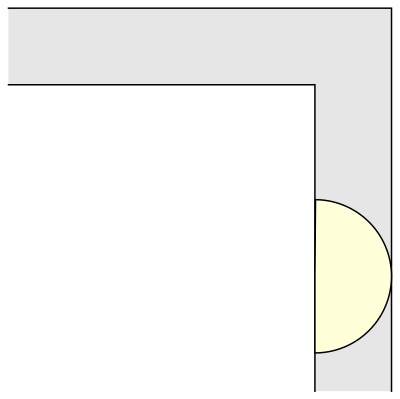
But what is the largest area that can be moved around?

Well, it has been conjectured that the shape with the largest area that one can move around a corner is known as “Gerver’s sofa”. And it looks like so:

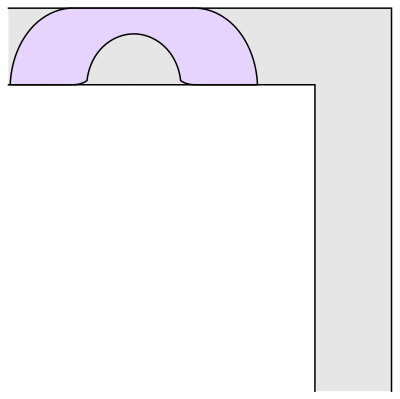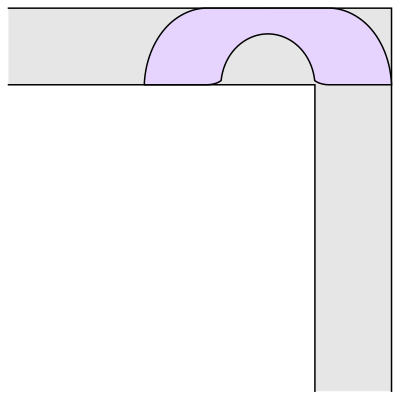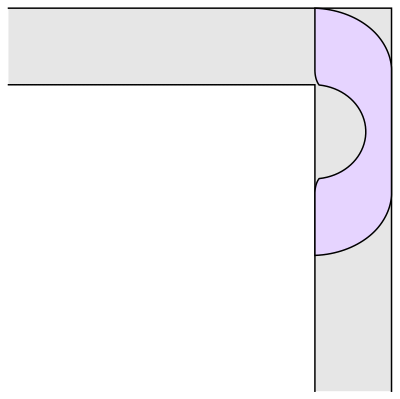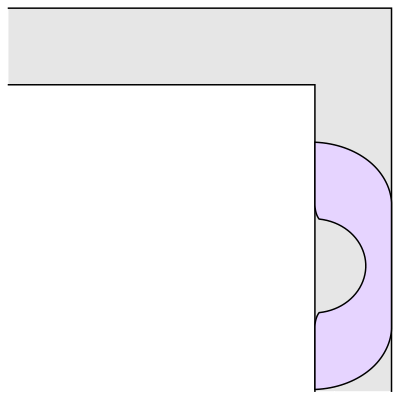
Wait.. Hang on a second

This sofa would only be effective for right handed turns. One can clearly see that if we have to turn left somewhere we would be kind of in a tough spot.

Prof.Romik from the University of California, Davis has proposed this shape popularly know as Romik’s ambidextrous sofa that solves this problem.

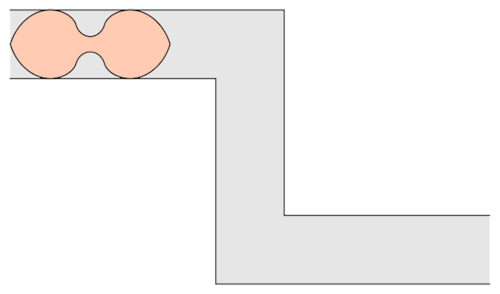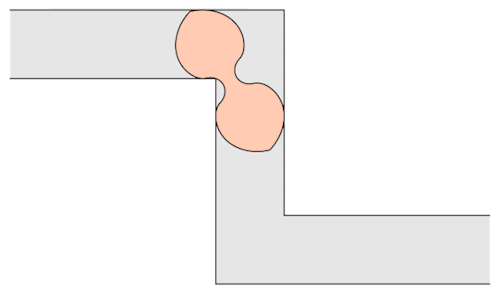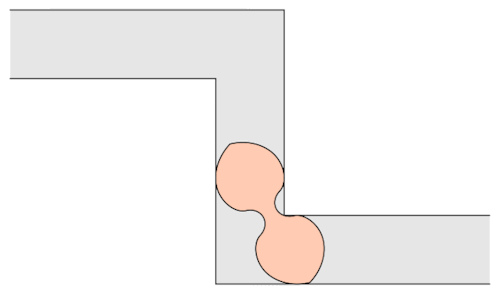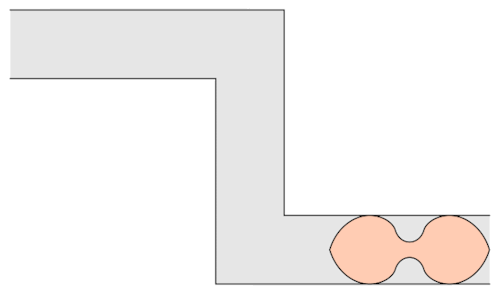
Although Prof.Romik’s sofa may/may not be the not the optimal solution, it is definitely is a breakthrough since this can pave the way for more complex ideas in mathematical analysis and more importantly sofa design.

Have a good one!

Luiz Sacilotto [Brazil] (1924-2003) ~ ‘C8752’, 1987. Acrylic and watercolor on canvas (89,9 x 89,9 cm).

Pois eu tbm tenho a dúvida se a partir do dia 17/12/2018 isso será permitido no TumBRL???

Now it’s time to play “is this a contour plot too racy for Tumblr?”