Wait.. Hang On A Second

If one remembers this particular episode from the popular sitcom ‘Friends’ where Ross is trying to carry a sofa to his apartment, it seems that moving a sofa up the stairs is ridiculously hard.
But life shouldn’t be that hard now should it?
The mathematician Leo Moser posed in 1966 the following curious mathematical problem: what is the shape of largest area in the plane that can be moved around a right-angled corner in a two-dimensional hallway of width 1? This question became known as the moving sofa problem, and is still unsolved fifty years after it was first asked.
The most common shape to move around a tight right angled corner is a square.
And another common shape that would satisfy this criterion is a semi-circle.
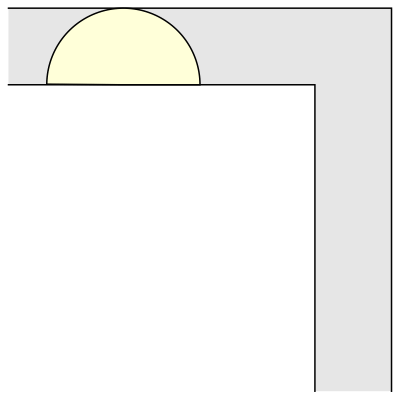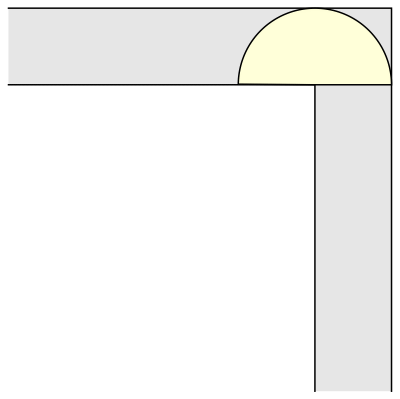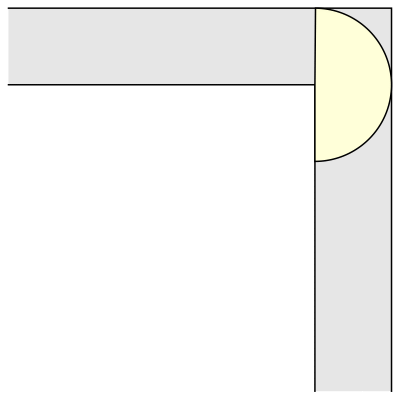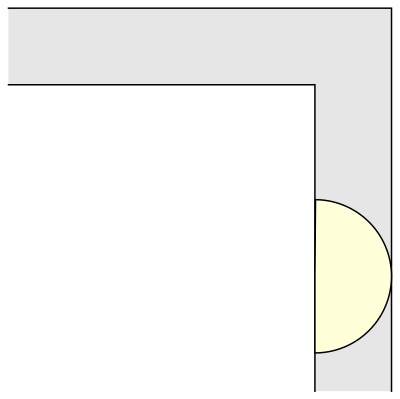
But what is the largest area that can be moved around?
Well, it has been conjectured that the shape with the largest area that one can move around a corner is known as “Gerver’s sofa”. And it looks like so:
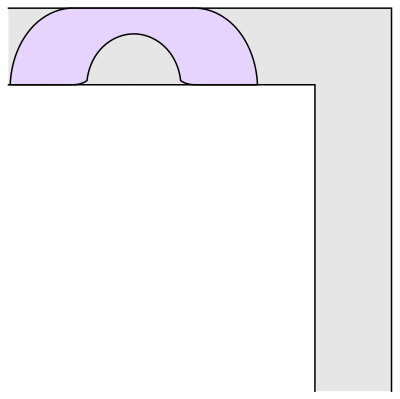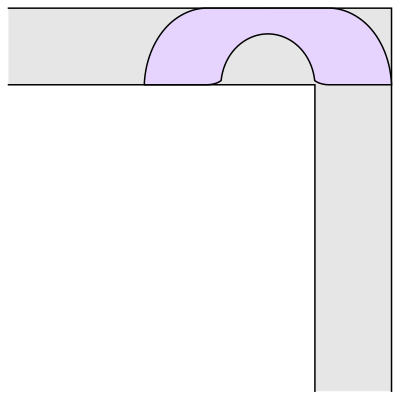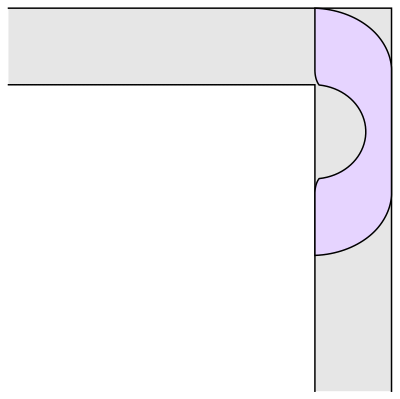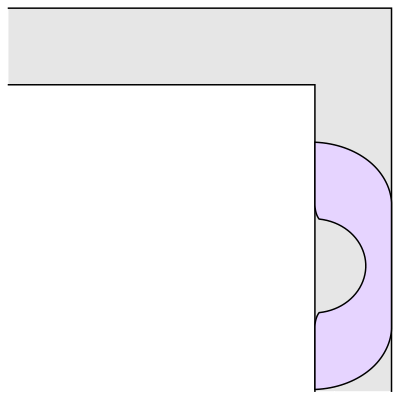
Wait.. Hang on a second
This sofa would only be effective for right handed turns. One can clearly see that if we have to turn left somewhere we would be kind of in a tough spot.
Prof.Romik from the University of California, Davis has proposed this shape popularly know as Romik’s ambidextrous sofa that solves this problem.
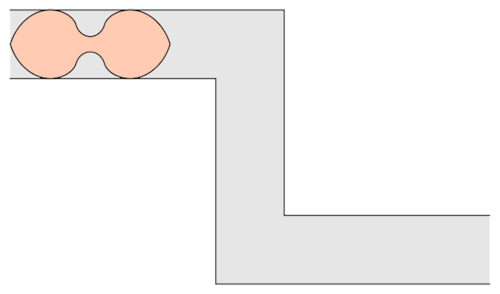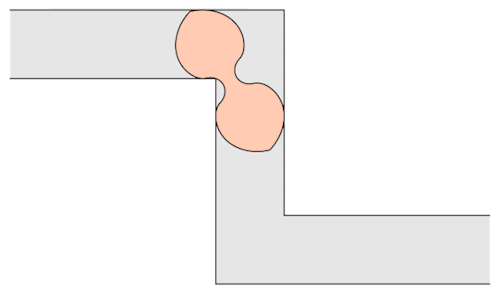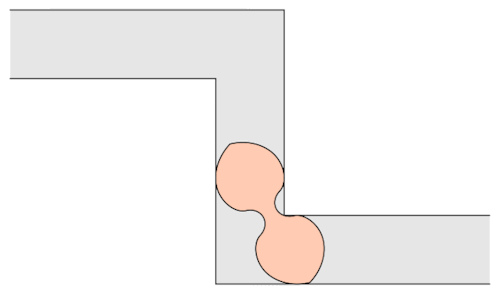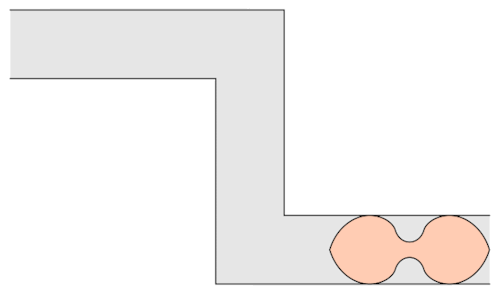
Although Prof.Romik’s sofa may/may not be the not the optimal solution, it is definitely is a breakthrough since this can pave the way for more complex ideas in mathematical analysis and more importantly sofa design.

Have a good one!
More Posts from Matematicaulysses and Others
👌👌😄



Toyota Matrix (matrix)
Essa animação é o mesmo modelo descrito na publicação abaixo 👇👇👇



Semi-regular polyhedra transformations.
These transformations are same as the models in this post.
Um belo gráfico 3D com a frequência das teclas mais usadas no inglês.
Só acho que o "espaço" é que seria uma das maiores.

Frequency of keyboard key usage

It’s a serious issue!
The regular hexagon hidden in a cube unfolds to a straight line on a net of the cube.




New Geometrically-Inspired Pastries, Cakes, and Sweets by Dinara Kasko
Shearer’s geometry puzzles
On his blog MathWithBadDrawings, Ben Orlin reposted a couple of geometrical sangaku-like puzzles by math teacher Catriona Shearer. These are eleven of her personal favorites. If you dare, definitely give them a try!

Transit Across a Purple Sun. What’s the total shaded area?

Shearer’s Emerald. Four squares. What’s the shaded area?

The Pyramid with Two Tombs. Two squares inside an equilateral triangle. What’s the angle?

Setting Sun, Rising Moon. What fraction of the rectangle is shaded?

Hex Hex Six. Both hexagons are regular. How long is the pink line?

Four, Three, Two. What’s the area of this triangle?

The Trinity Quartet. All four triangles are equilateral. What fraction of the rectangle do they cover?

The Falling Domino. This design is made of three 2×1 rectangles. What fraction of it is shaded?

Slices in a Sector. The three colored sections here have the same area. What’s the total area of the square?
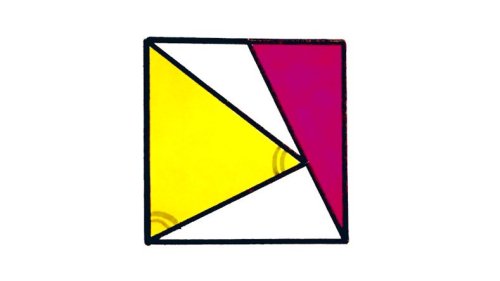
Disorientation. The right-angled triangle covers ¼ of the square. What fraction does the isosceles triangle cover?

Sunny Smile Up. What fraction of the circle is shaded?


Bruno Munari, (1960), The Square, Translation by corrainiStudio, Corraini Edizioni, Mantova, (2006-)2011, pp. 62-63
Basic definition of a tangent line.


-
 anbarbam liked this · 5 months ago
anbarbam liked this · 5 months ago -
 againstadarkbackground liked this · 8 months ago
againstadarkbackground liked this · 8 months ago -
 drumpenguin reblogged this · 8 months ago
drumpenguin reblogged this · 8 months ago -
 bobertflaming reblogged this · 8 months ago
bobertflaming reblogged this · 8 months ago -
 small-cog reblogged this · 1 year ago
small-cog reblogged this · 1 year ago -
 tomicaleto reblogged this · 1 year ago
tomicaleto reblogged this · 1 year ago -
 thisisnotjuli reblogged this · 1 year ago
thisisnotjuli reblogged this · 1 year ago -
 itsawritblr liked this · 1 year ago
itsawritblr liked this · 1 year ago -
 thousand-years-dreaming reblogged this · 1 year ago
thousand-years-dreaming reblogged this · 1 year ago -
 itpiercesskin liked this · 1 year ago
itpiercesskin liked this · 1 year ago -
 thebottomleftcorner reblogged this · 1 year ago
thebottomleftcorner reblogged this · 1 year ago -
 eternalcyclicality reblogged this · 1 year ago
eternalcyclicality reblogged this · 1 year ago -
 lowgardn liked this · 1 year ago
lowgardn liked this · 1 year ago -
 djlunchbox reblogged this · 1 year ago
djlunchbox reblogged this · 1 year ago -
 djlunchbox liked this · 1 year ago
djlunchbox liked this · 1 year ago -
 tolsunflowerboi reblogged this · 1 year ago
tolsunflowerboi reblogged this · 1 year ago -
 tolsunflowerboi liked this · 1 year ago
tolsunflowerboi liked this · 1 year ago -
 hazelgardener liked this · 1 year ago
hazelgardener liked this · 1 year ago -
 nspcritterstuck reblogged this · 1 year ago
nspcritterstuck reblogged this · 1 year ago -
 nspcritterstuck liked this · 1 year ago
nspcritterstuck liked this · 1 year ago -
 208tinyhorses reblogged this · 1 year ago
208tinyhorses reblogged this · 1 year ago -
 lea-winterregen liked this · 1 year ago
lea-winterregen liked this · 1 year ago -
 chrisisjustalie reblogged this · 1 year ago
chrisisjustalie reblogged this · 1 year ago -
 buckyandsteeb liked this · 1 year ago
buckyandsteeb liked this · 1 year ago -
 swhitegirlproblems reblogged this · 1 year ago
swhitegirlproblems reblogged this · 1 year ago -
 robin-sends-it liked this · 1 year ago
robin-sends-it liked this · 1 year ago -
 deltadizzy reblogged this · 1 year ago
deltadizzy reblogged this · 1 year ago -
 deltadizzy liked this · 1 year ago
deltadizzy liked this · 1 year ago -
 beveverage reblogged this · 1 year ago
beveverage reblogged this · 1 year ago -
 beveverage liked this · 1 year ago
beveverage liked this · 1 year ago -
 rebloggingcomet reblogged this · 1 year ago
rebloggingcomet reblogged this · 1 year ago -
 thefallencomet liked this · 1 year ago
thefallencomet liked this · 1 year ago -
 game-shy liked this · 1 year ago
game-shy liked this · 1 year ago -
 peachpunc liked this · 1 year ago
peachpunc liked this · 1 year ago -
 cock-lore liked this · 1 year ago
cock-lore liked this · 1 year ago -
 the-shadow-83 reblogged this · 1 year ago
the-shadow-83 reblogged this · 1 year ago -
 histories-and-mystery reblogged this · 1 year ago
histories-and-mystery reblogged this · 1 year ago -
 incurablebookwyrm liked this · 1 year ago
incurablebookwyrm liked this · 1 year ago -
 inlovewithanathemadevice liked this · 1 year ago
inlovewithanathemadevice liked this · 1 year ago -
 uss-genderprise liked this · 1 year ago
uss-genderprise liked this · 1 year ago -
 lesbianminou reblogged this · 1 year ago
lesbianminou reblogged this · 1 year ago -
 captainbookwyrm reblogged this · 1 year ago
captainbookwyrm reblogged this · 1 year ago -
 rubixpsyche liked this · 1 year ago
rubixpsyche liked this · 1 year ago -
 foryouthegays reblogged this · 1 year ago
foryouthegays reblogged this · 1 year ago -
 kandyroro liked this · 1 year ago
kandyroro liked this · 1 year ago -
 somewhatcompetent reblogged this · 1 year ago
somewhatcompetent reblogged this · 1 year ago -
 freerealestateforjim reblogged this · 1 year ago
freerealestateforjim reblogged this · 1 year ago -
 freerealestateforjim liked this · 1 year ago
freerealestateforjim liked this · 1 year ago
Blog do profº Ulysses TDBueno destinado a curiosidades, demonstrações, links, trabalhos, artigos, imagens e tudo que possa mostrar a matemática no mundo.
107 posts