Maurits Cornelis Escher (Dutch, 1898-1972) - Encounter, Lithograph On Paper, 46.99 X 57.15 Cm (1944)

Just Descending

Can’t find the creator of this. I saw it tweeted by Alexander Bogomolny. It’s Escher, of course, but also the Penrose staircase. Roger and his father! Great #mathart story. See Wikipedia for more.

I really enjoy your postings. I would like to build some of the models you have built. How do you build the joints that fasten the staws together in the isocosahedron for October 27, 2017? Is it part of a kit? Where can I get them? Thank you so much!

Thanks!

I guess this post, right?(Accurately, I post this on Oct 17, not Oct 27)

I bought this kit at IKEA and 100-yen shop.

Here are how I made the model. :D

I made cuboctahedron and icosidodecahedron models too.(Octahedron model is the previous one)

These transforms rhombicuboctahedron, rhombicosidodecahedron and cuboctahedron.

So many parts and monotonous work, but interesting. :D

'Endless Loop'. Max Bill. 1953-1956.

If one remembers this particular episode from the popular sitcom ‘Friends’ where Ross is trying to carry a sofa to his apartment, it seems that moving a sofa up the stairs is ridiculously hard.

But life shouldn’t be that hard now should it?

The mathematician Leo Moser posed in 1966 the following curious mathematical problem: what is the shape of largest area in the plane that can be moved around a right-angled corner in a two-dimensional hallway of width 1? This question became known as the moving sofa problem, and is still unsolved fifty years after it was first asked.

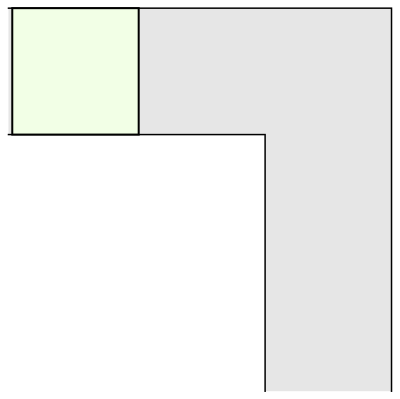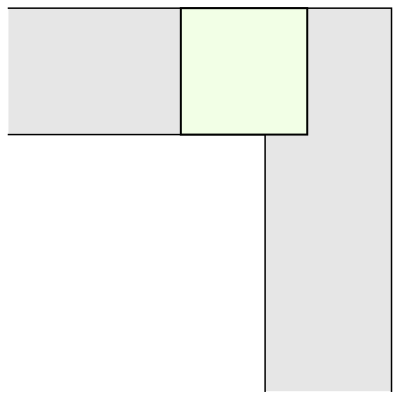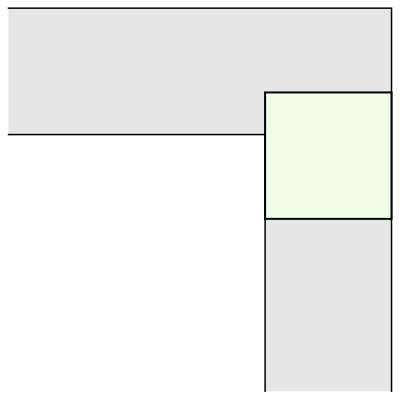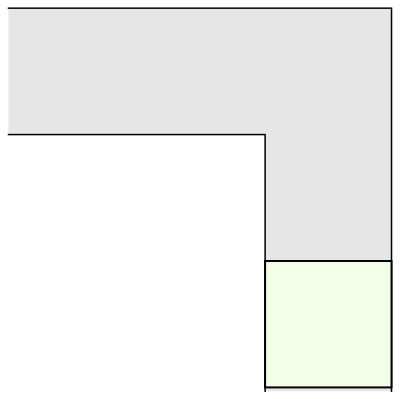
The most common shape to move around a tight right angled corner is a square.

And another common shape that would satisfy this criterion is a semi-circle.

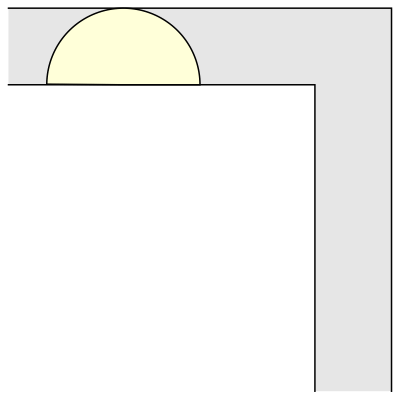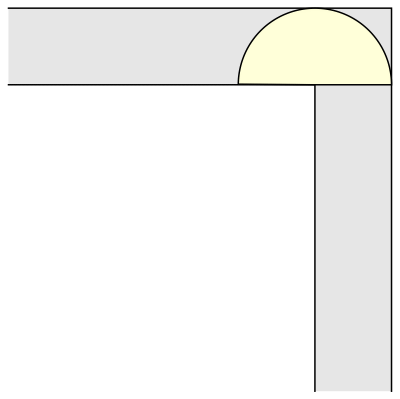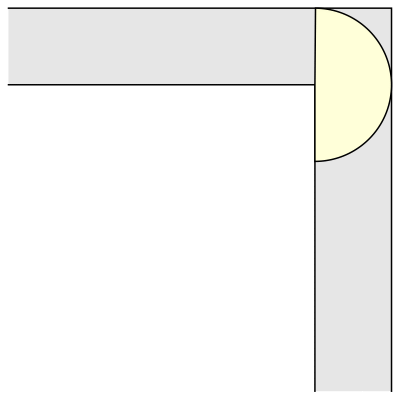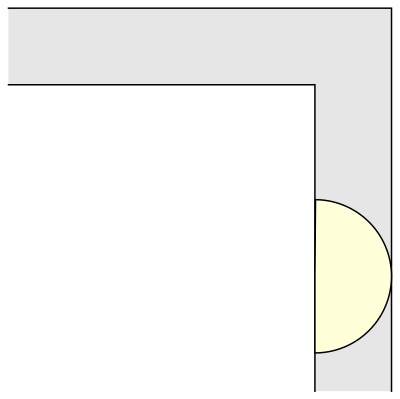
But what is the largest area that can be moved around?

Well, it has been conjectured that the shape with the largest area that one can move around a corner is known as “Gerver’s sofa”. And it looks like so:

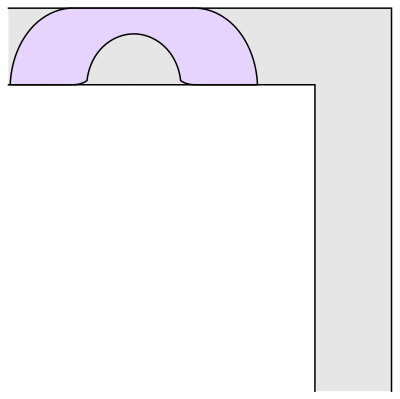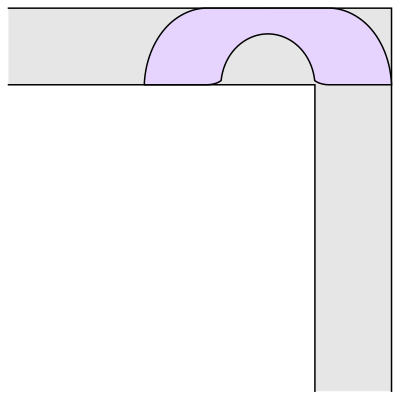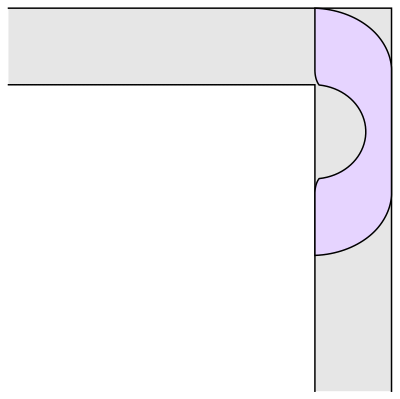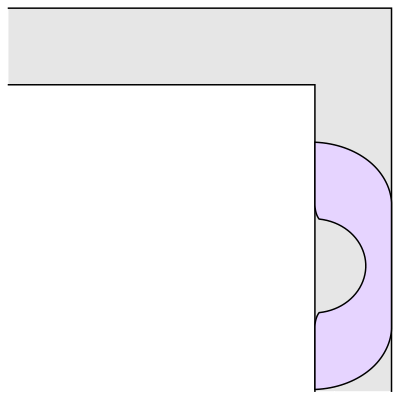
Wait.. Hang on a second

This sofa would only be effective for right handed turns. One can clearly see that if we have to turn left somewhere we would be kind of in a tough spot.

Prof.Romik from the University of California, Davis has proposed this shape popularly know as Romik’s ambidextrous sofa that solves this problem.

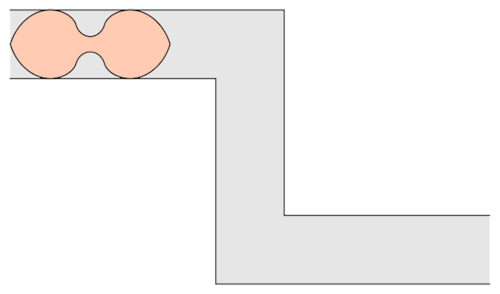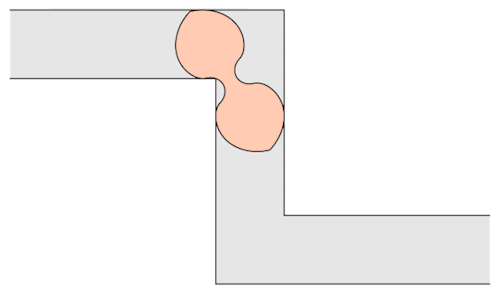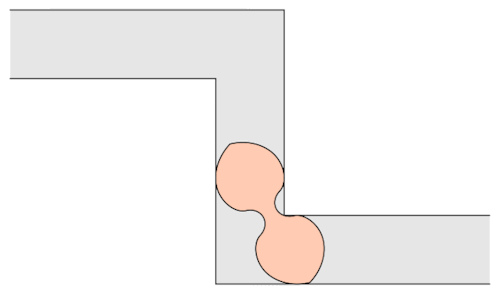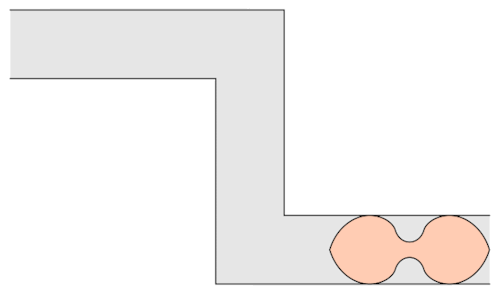
Although Prof.Romik’s sofa may/may not be the not the optimal solution, it is definitely is a breakthrough since this can pave the way for more complex ideas in mathematical analysis and more importantly sofa design.

Have a good one!

whoa this guy knows how to party

The secret of pie

myalltimenews.blogspot.com

What Fraction Is Shaded? Challenge From The UK

What Fraction Is Shaded? Challenge From The UK This is a really fun geometry problem. It comes from the UKMT, a test which is part of f

Um probleminha divertido de geometria plana.