😭😭😭
😭😭😭
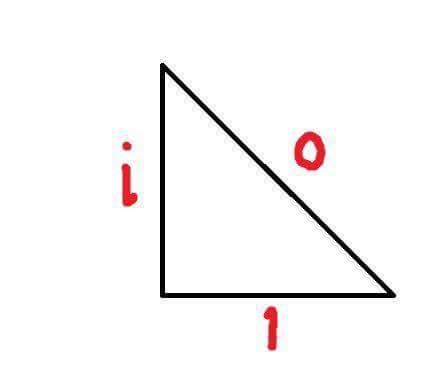
More Posts from Matematicaulysses and Others
Piada bilíngue:
Sabe por que a formiga tem 4 patas? Porque se ela tivesse 5 seria uma Fivemiga... 🤣😋😂😆😎😉
More on the Spectre
Images from this great Yoshiaki Araki thread. (If you're interested in tessellations and are twitterpated, he's a must follow.)





He links the Nature article (good and a free read).
Best one, so far:

Robert Farthauer suggests:

And, of course, the actual article, by David Smith, Joseph Samuel Myers, Craig S. Kaplan, and Chaim Goodman-Strauss.
Kaplan gives this illustration of the tile:

He has a one page stop for info about the tiling.
Bonus: via New-Cleckit Dominie


Rblue = (Rgreen + Rred) / 2

Simple. Coolllllll

hm (via complex form)




New Geometrically-Inspired Pastries, Cakes, and Sweets by Dinara Kasko


💙💜❤️ BI? PI! ❤️💜💙
The 120-cell.
You probably think dodecahedra are tight. Have you considered trying hyperdodecahedra?
Great thanks to Professor Mark Crawford, who showed me this gem. It may take a little bit to shatter your consciousness, so please be patient. :)
Dodecaplex. Polydodecahedron. Hecatonicosachoron. Dodecacontachoron. Hecatonicosahedroid.
Mathematics is beautiful. <3
The Complex Geometry of Islamic Design
In Islamic culture, geometry is everywhere. You can find it in mosques, madrasas, palaces and private homes. This tradition began in the 8th century CE during the early history of Islam, when craftsman took preexisting motifs from Roman and Persian cultures and developed them into new forms of visual expression.

This period of history was a golden age of Islamic culture, during which many achievements of previous civilizations were preserved and further developed, resulting in fundamental advancements in scientific study and mathematics. Accompanying this was an increasingly sophisticated use of abstraction and complex geometry in Islamic art, from intricate floral motifs adorning carpets and textiles, to patterns of tile work that seemed to repeat infinitely, inspiring wonder and contemplation of eternal order.

Despite the remarkable complexity of these designs, they can be created with just a compass to draw circles and a ruler to make lines within them, and from these simple tools emerges a kaleidoscope multiplicity of patterns. So how does that work? Well, everything starts with a circle. The first major decision is how will you divide it up? Most patterns split the circle into four, five or six equal sections. And each division gives rise to distinctive patterns.

There’s an easy way to determine whether any pattern is based on fourfold, fivefold, or sixfold symmetry. Most contain stars surrounded by petal shapes. Counting the number of rays on a starburst, or the number of petals around it, tells us what category the pattern falls into. A star with six rays, or surrounded by six petals, belongs in the sixfold category. One with eight petals is part of the fourfold category, and so on.

There’s another secret ingredient in these designs: an underlying grid. Invisible, but essential to every pattern, the grid helps determine the scale of the composition before work begins, keeps the pattern accurate, and facilitates the invention of incredible new patterns. Let’s look at an example of how these elements come together.

We’ll start with a circle within a square, and divide it into eight equal parts. We can then draw a pair of criss-crossing lines and overlay them with another two. These lines are called construction lines, and by choosing a set of their segments, we’ll form the basis of our repeating pattern.

Many different designs are possible from the same construction lines just by picking different segments. And the full pattern finally emerges when we create a grid with many repetitions of this one tile in a process called tessellation.

By choosing a different set of construction lines, we might have created this any of the above patterns. The possibilities are virtually endless.

We can follow the same steps to create sixfold patterns by drawing construction lines over a circle divided into six parts, and then tessellating it, we can make something like the above.

Here’s another sixfold pattern that has appeared across the centuries and all over the Islamic world, including Marrakesh, Agra, Konya and the Alhambra.

Fourfold patterns fit in a square grid, and sixfold patterns in a hexagonal grid.

Fivefold patterns, however, are more challenging to tessellate because pentagons don’t neatly fill a surface, so instead of just creating a pattern in a pentagon, other shapes have to be added to make something that is repeatable, resulting in patterns that may seem confoundingly complex, but are still relatively simple to create.

This more than 1,000-year-old tradition has wielded basic geometry to produce works that are intricate, decorative and pleasing to the eye. And these craftsman prove just how much is possible with some artistic intuition, creativity, dedication along with a great compass and ruler.

If one remembers this particular episode from the popular sitcom ‘Friends’ where Ross is trying to carry a sofa to his apartment, it seems that moving a sofa up the stairs is ridiculously hard.
But life shouldn’t be that hard now should it?
The mathematician Leo Moser posed in 1966 the following curious mathematical problem: what is the shape of largest area in the plane that can be moved around a right-angled corner in a two-dimensional hallway of width 1? This question became known as the moving sofa problem, and is still unsolved fifty years after it was first asked.
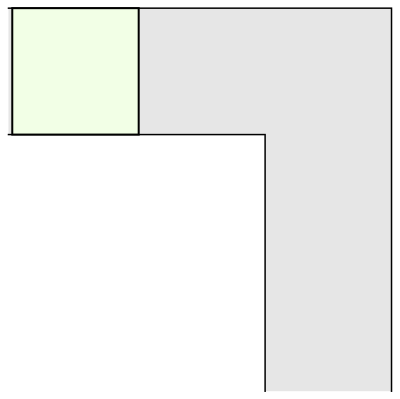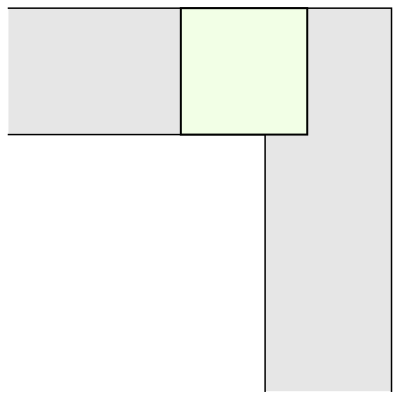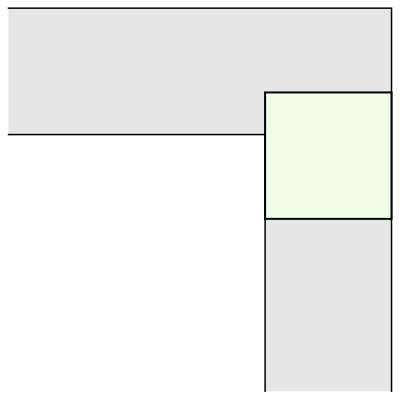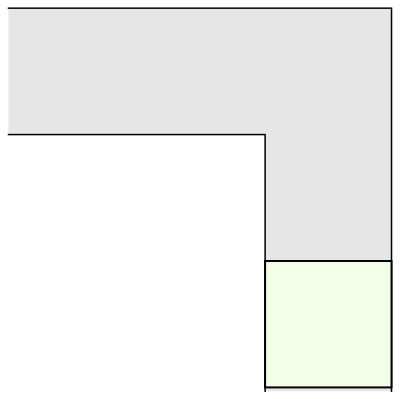
The most common shape to move around a tight right angled corner is a square.
And another common shape that would satisfy this criterion is a semi-circle.
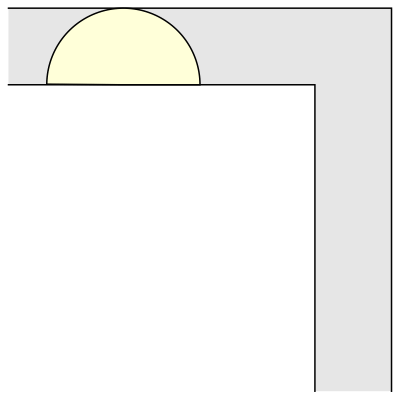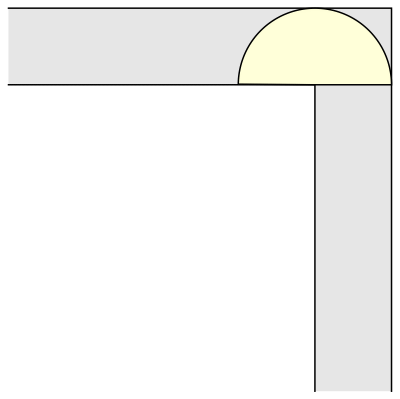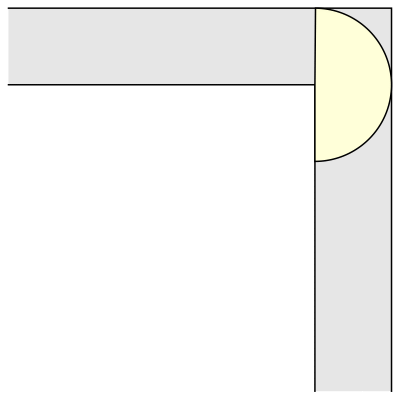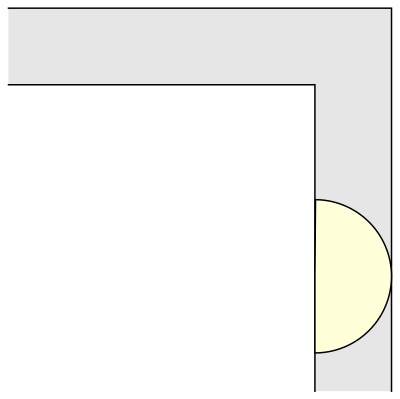
But what is the largest area that can be moved around?
Well, it has been conjectured that the shape with the largest area that one can move around a corner is known as “Gerver’s sofa”. And it looks like so:
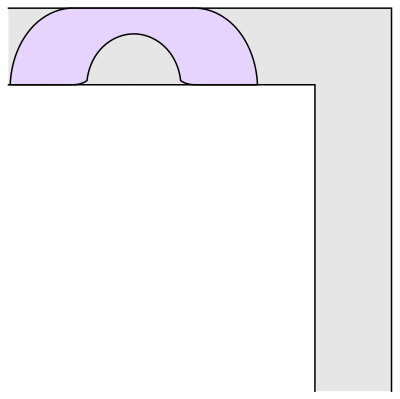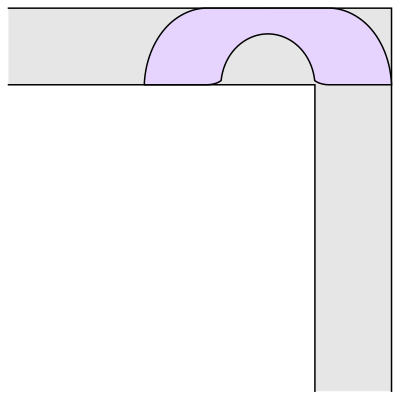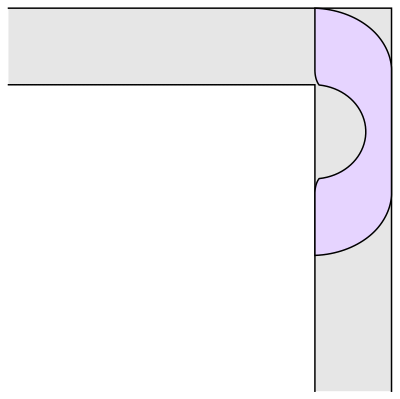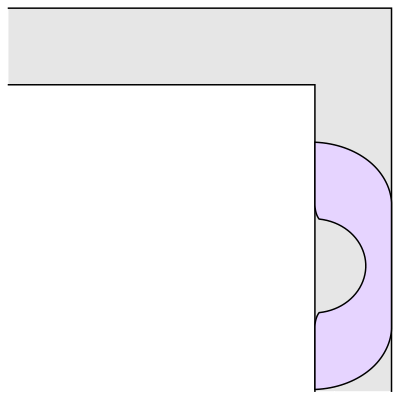
Wait.. Hang on a second
This sofa would only be effective for right handed turns. One can clearly see that if we have to turn left somewhere we would be kind of in a tough spot.
Prof.Romik from the University of California, Davis has proposed this shape popularly know as Romik’s ambidextrous sofa that solves this problem.
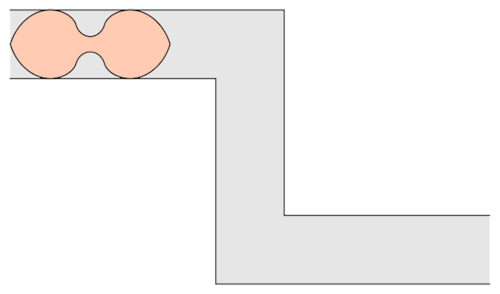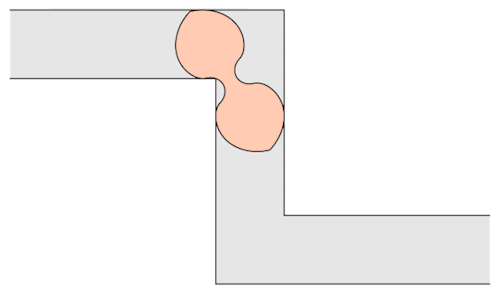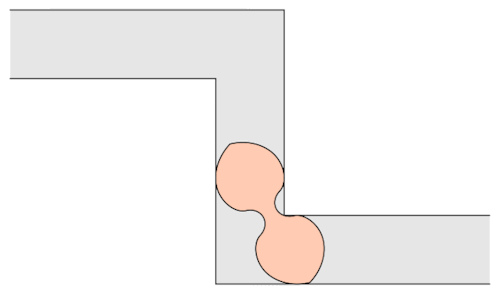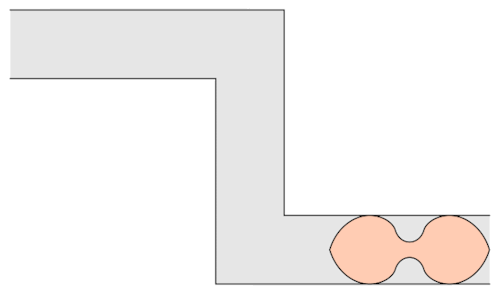
Although Prof.Romik’s sofa may/may not be the not the optimal solution, it is definitely is a breakthrough since this can pave the way for more complex ideas in mathematical analysis and more importantly sofa design.

Have a good one!
-
 mehanios reblogged this · 2 months ago
mehanios reblogged this · 2 months ago -
 secret-h reblogged this · 3 months ago
secret-h reblogged this · 3 months ago -
 theworldtravellingteenager liked this · 3 months ago
theworldtravellingteenager liked this · 3 months ago -
 sidereon-spaceace reblogged this · 3 months ago
sidereon-spaceace reblogged this · 3 months ago -
 mehanios reblogged this · 3 months ago
mehanios reblogged this · 3 months ago -
 tachvintlogic reblogged this · 3 months ago
tachvintlogic reblogged this · 3 months ago -
 pinkpeccary reblogged this · 3 months ago
pinkpeccary reblogged this · 3 months ago -
 52frogs reblogged this · 3 months ago
52frogs reblogged this · 3 months ago -
 gas-station-clown reblogged this · 3 months ago
gas-station-clown reblogged this · 3 months ago -
 gas-station-clown liked this · 3 months ago
gas-station-clown liked this · 3 months ago -
 secret-h liked this · 3 months ago
secret-h liked this · 3 months ago -
 beep-beep-kneecaps reblogged this · 3 months ago
beep-beep-kneecaps reblogged this · 3 months ago -
 nakiteers liked this · 3 months ago
nakiteers liked this · 3 months ago -
 willshaper liked this · 3 months ago
willshaper liked this · 3 months ago -
 ohmyoverland liked this · 3 months ago
ohmyoverland liked this · 3 months ago -
 that-dog-is-a-storming-hero liked this · 3 months ago
that-dog-is-a-storming-hero liked this · 3 months ago -
 whalerrat reblogged this · 3 months ago
whalerrat reblogged this · 3 months ago -
 joetrohwiththefro liked this · 3 months ago
joetrohwiththefro liked this · 3 months ago -
 dark66angels reblogged this · 3 months ago
dark66angels reblogged this · 3 months ago -
 dark66angels liked this · 3 months ago
dark66angels liked this · 3 months ago -
 peachdoxie reblogged this · 3 months ago
peachdoxie reblogged this · 3 months ago -
 kinddogg reblogged this · 3 months ago
kinddogg reblogged this · 3 months ago -
 kinddogg liked this · 3 months ago
kinddogg liked this · 3 months ago -
 gostaks reblogged this · 3 months ago
gostaks reblogged this · 3 months ago -
 garlend liked this · 3 months ago
garlend liked this · 3 months ago -
 raginrayguns reblogged this · 3 months ago
raginrayguns reblogged this · 3 months ago -
 mrcatfishing reblogged this · 5 months ago
mrcatfishing reblogged this · 5 months ago -
 mrcatfishing liked this · 5 months ago
mrcatfishing liked this · 5 months ago -
 goblincharbelcher liked this · 7 months ago
goblincharbelcher liked this · 7 months ago -
 requiem2007 liked this · 7 months ago
requiem2007 liked this · 7 months ago -
 molecularhomosexual liked this · 7 months ago
molecularhomosexual liked this · 7 months ago -
 perestroika-hilton reblogged this · 7 months ago
perestroika-hilton reblogged this · 7 months ago -
 cant-think-of-a-good-one liked this · 8 months ago
cant-think-of-a-good-one liked this · 8 months ago -
 i-iii-iii-vii liked this · 1 year ago
i-iii-iii-vii liked this · 1 year ago -
 sunless-not-sinless liked this · 1 year ago
sunless-not-sinless liked this · 1 year ago -
 leotraccaconte liked this · 1 year ago
leotraccaconte liked this · 1 year ago -
 mystics-rp-central liked this · 2 years ago
mystics-rp-central liked this · 2 years ago -
 lostinthatsauce liked this · 2 years ago
lostinthatsauce liked this · 2 years ago -
 azdoine liked this · 3 years ago
azdoine liked this · 3 years ago -
 flowers-all-around-me reblogged this · 3 years ago
flowers-all-around-me reblogged this · 3 years ago -
 shyjoghurteater reblogged this · 3 years ago
shyjoghurteater reblogged this · 3 years ago -
 generic-waffle reblogged this · 3 years ago
generic-waffle reblogged this · 3 years ago -
 because-im-real liked this · 3 years ago
because-im-real liked this · 3 years ago -
 universeusurper reblogged this · 3 years ago
universeusurper reblogged this · 3 years ago -
 fishgut reblogged this · 3 years ago
fishgut reblogged this · 3 years ago -
 hydrawolfy reblogged this · 3 years ago
hydrawolfy reblogged this · 3 years ago -
 hydrawolfy liked this · 3 years ago
hydrawolfy liked this · 3 years ago -
 spursthatjinglejanglejingle liked this · 3 years ago
spursthatjinglejanglejingle liked this · 3 years ago
Blog do profº Ulysses TDBueno destinado a curiosidades, demonstrações, links, trabalhos, artigos, imagens e tudo que possa mostrar a matemática no mundo.
107 posts