Fields Of Mathematics
fields of mathematics
number theory: The Queen of Mathematics, in that it takes a lot from other fields and provides little in return, and people are weirdly sentimental about it.
combinatorics: Somehow simultaneously the kind of people who get really excited about Martin Gardner puzzles and very serious no-nonsense types who don’t care about understanding why something is true as long as they can prove that it’s true.
algebraic geometry: Here’s an interesting metaphor, and here’s several thousand pages of work fleshing it out.
differential geometry: There’s a lot of really cool stuff built on top of a lot of boring technical details, but they frequently fill entire textbooks or courses full of just the boring stuff, and they seem to think students will find this interesting in itself rather than as a necessary prerequisite to something better. So there’s definitely something wrong with them.
category theory: They don’t really seem to understand that the point of generalizing a result is so that you can apply it to other situations.
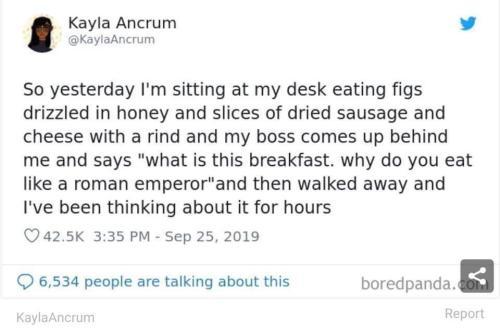
differential equations: physicists
real analysis: What if we took the most boring parts of a proof and just spent all our time studying those?
point-set topology: See real analysis, but less relevant to the real world.
complex analysis: Sorcery. I thought it seemed like sorcery because I didn’t know much about it, but then I learned more, and now the stuff I learned just seems like sorcery that I know how to do.
algebraic topology: Some of them are part of a conspiracy with category theorists to take over mathematics. I’m pretty sure that most algebraic topologists aren’t involved in that, but I don’t really know what else they’re up to.
functional analysis: Like real analysis but with category theorists’ generalization fetish.
group theory: Probably masochists? It’s hard to imagine how else someone could be motivated to read a thousand-page paper, let alone write one.
operator algebras: Seems cool but I can’t understand a word of it, so I can’t be sure they’re not just bullshitting the whole thing.
commutative/homological algebra: Diagram chases are of the devil, and these people are his worshipers.
More Posts from Bsdndprplplld and Others
ok now i might have some kind of super memory??
a week ago i played chess with bf and we didn't finish, so now i arranged the board as i remembered it and i got 13 out of 14 pieces correctly
i mean wow i didn't know i am capable of something like this
might be autism i suspect i might have
anyway now i want to know everything about human memory and take advantage of that
I know your thesis was about something to do with algebraic topology, may I ask what exactly it was about?
(and congrats to you getting your bachelors degree and into a masters program)
(thank you!)
my thesis was about an open question regarding a certain skein module of tangles on 2n nodes. the conjecture is that the module is free and in my thesis I constructed a generating set that is free for n=2,3 (direct calculation) but I have yet to prove that for a general n. if you are interested I can send you the paper in which the question was posed, all the details are explained there and would be hard to write down here without tex lol
just had a reflection about perfectionism. today I had an exam for which I was prepared very well, but my stupid brain happened and I didn't get the highest grade. my boyfriend was comforting me and he asked since when I want to ace everything, this question made me think
indeed, I don't want to ace everything. I am taking 4 courses this semester, one of which I don't care about enough to strive for the best grade, one of which is way too hard to aim that far, two of which I thought were achievable. and now I didn't achieve that. it feels different to set unrealistic goals and then never achieve them than to set very realistic ones and still fail, that's what I realized today
I am not a perfectionist. I used to be, years ago, and then I learned to set realistic goals. now I'm thinking, isn't perfectionism a kind of a coping mechanism? deep down you know your goals are impossible, so it's not really surprising when you fail. you are never satisfied, sure, but maybe it does feel more safe this way than to not know if you will be satisfied or disappointed. if that's the case then setting realistic goals is absolutely not the way to heal perfectionism
"numbers don't lie" the real numbers are literally a lie group
Mathematicians be like:
Def 1.1: A function f is fucked-up iff it is not Lebesgue measurable
Def 1.2: A function is evil iff its graph has non-integer Hausdorff dimension.
Exercise 1: Prove that there exist fucked-up and evil functions
I'm reblogging this to compare it later with 1.A from Hatcher's Algebraic Topology. in that chapter he defines the topology on a graph if anyone else wants to check it out
Intuitively, it seems to me that graphs should be some sort of finite topological space. I mean, topology studies "how spaces are connected to themselves", and a graph represents a finite space of points with all the internal connections mapped out. That sounds topological to me! And of course many people consider the Seven Bridges of Königsberg problem to be the "beginning" of topology, and that's a graph theory problem. So graphs should be topological spaces.
Now, I vaguely remember searching for this before and finding out that they aren't, but I decided to investigate for myself. After a bit of thought, it turns out that graphs can't be topological spaces while preserving properties that we would intuitively want. Here's (at least one of the reasons) why:
We want to put some topology on the vertices of our graph such that graph-theoretic properties and topological properties line up—of particular relevance here, we want graph-theoretic connectedness to line up with topological connectedness. But consider the following pair of graphs on four vertices:

On the left is the co-paw graph, and on the right is the cycle graph C_4.
Graph theoretically, the co-paw graph has two connected components, and C_4 has only one. Now consider the subgraph {A, D} of the co-paw graph. Graph theoretically, it is disconnected, and if we want it to also be topologically disconnected, it must by definition be the union of two disjoint open sets. Therefore, in whatever topology we put on this graph, {A} and {D} must be open. The same argument shows that {B} and {C} must be open as well. Therefore the topology on the co-paw graph must be the discrete topology.
Now consider the subgraph {B, D} of C_4. It is disconnected, so again {B} and {D} must be open. Since {A, C} is also disconnected, {A} and {C} must be open. So the topology on C_4 must again be the discrete topology.
But these graphs aren't isomorphic! So they definitely shouldn't have the same topology.
It is therefore impossible to put a topology on the points of a graph such that its graph-theoretic properties line up with its topological properties.
Kind of disappointing TBH.

i’m starting a collection
13 IX 2022
my euclidean geometry journey will be over soon and the start of the semester is so close, it's kinda scary
recently I stumbled upon someone's post with a time-lapse video of their study session. I liked it so much that I decided to make mine
this is me learning about the snake lemma and excision
the excision theorem is the hardest one in homology so far btw, I spent about 4 hours on it and I am barely halfway through. I like the idea of the proof tho, it's very intuitive actually: start simple and tangible, then complicate with each step lmao
I realized two things recently. one of them is that deeply studying theorems is important and effective. effective, uh? in what way? in exams we don't need to cite the whole proof, it suffices to say "the assertion follows from the X theorem"
yeah right, but my goal is to be a researcher, not a good test-taker, researchers create their own proofs and what's better than studying how others did it if I am for now unable to produce original content in math?
the second things is that I learned how to pay attention. I know, it sounds crazy, but I've been trying another ✨adhd medication✨ and after a while I realized that paying attention is exhausting, but this is the only way to really learn something new, not just repeat what I already know. it made me see how much energy and effort it takes to make good progress and that it is necessary to invest so much
I am slowly learning to control my attention, which brings a lot of hope, as I believed that I had to rely on random bouts of hyperfocus, before I started treatment. I am becoming more aware or how much I am focusing at the given moment and I'm trying to work on optimizing those levels. for instance, when I'm reading a chapter in a textbook for the first time, it is necessary to remember every single detail, but wanting to do so consumes a lot of energy, because it means paying constant attention. it is ineffective because most likely I will have to repeat the process a few more times before I truly retain everything. being able to actually pay attention at will sure does feel good tho, as if I had a new part of my brain unlocked
I am solving more exercises for algebraic topology, procrastinating my lecture prep lmao. I am supposed to talk about the power of a point and radical axes, I have a week left and I can't force myself to start, because there is so much good stuff to do instead

I have a dream to produce some original results in my bachelor's thesis. it may be very difficult, because I hardly know anything, that's why I'm calling it a dream, not a goal. the plan is to start writing at the end of the semester, submit sometime in june
I spent last week at the seminar on analysis and oh boi, I will have to think twice next time someone asks if I like analysis. the lecturer who taught me at uni had a different approach than the "classic" one. we did a little bit of differential geometry, Lie groups and de Rham cohomology, those are the things I like. meanwhile at the seminar it was mostly about analytic methods of PDEs, the most boring shit I have ever seen
complex analysis will most likely be enjoyable tho, I'm taking the course this semester
for the next few days I need to force myself to prep that damn geometry lecture. other than that I plan to keep solving the AT exercises and maybe learn some more commutative algebra. I wish everyone a pleasant almost-autumn day 🍁
7-9 VIII 2021
did math and coding nothing special really
sleep: good
concentration: good
phone time: good
reading about measure theory. here is a great book:

everything is so well explained here. i wish i could do more math than i have time for but i guess it's fine, it's holidays, i will wreck my brain completely anyway when october comes
tomorrow more measure theory and topo
-
 middlering reblogged this · 4 months ago
middlering reblogged this · 4 months ago -
 dynmaxblaze liked this · 11 months ago
dynmaxblaze liked this · 11 months ago -
 cythereafemme liked this · 1 year ago
cythereafemme liked this · 1 year ago -
 thebewilderer reblogged this · 1 year ago
thebewilderer reblogged this · 1 year ago -
 emmmidk reblogged this · 1 year ago
emmmidk reblogged this · 1 year ago -
 apocalypticautumn liked this · 1 year ago
apocalypticautumn liked this · 1 year ago -
 tangible-witchiness liked this · 1 year ago
tangible-witchiness liked this · 1 year ago -
 thegrayearloftea liked this · 1 year ago
thegrayearloftea liked this · 1 year ago -
 nichooo liked this · 1 year ago
nichooo liked this · 1 year ago -
 notbranch liked this · 1 year ago
notbranch liked this · 1 year ago -
 not-hiesenberg liked this · 1 year ago
not-hiesenberg liked this · 1 year ago -
 coyotecalculations liked this · 1 year ago
coyotecalculations liked this · 1 year ago -
 flowers-all-around-me liked this · 2 years ago
flowers-all-around-me liked this · 2 years ago -
 ulysses-but-somehow-more-transer reblogged this · 2 years ago
ulysses-but-somehow-more-transer reblogged this · 2 years ago -
 halaagmod liked this · 2 years ago
halaagmod liked this · 2 years ago -
 processes reblogged this · 2 years ago
processes reblogged this · 2 years ago -
 copingwithexistence liked this · 2 years ago
copingwithexistence liked this · 2 years ago -
 snowdroprd-moved liked this · 2 years ago
snowdroprd-moved liked this · 2 years ago -
 hmmmmmmmmm111116 liked this · 2 years ago
hmmmmmmmmm111116 liked this · 2 years ago -
 awkwardtuatara liked this · 2 years ago
awkwardtuatara liked this · 2 years ago -
 venusfigurine liked this · 2 years ago
venusfigurine liked this · 2 years ago -
 omb12 liked this · 2 years ago
omb12 liked this · 2 years ago -
 notosct liked this · 2 years ago
notosct liked this · 2 years ago -
 ring-theory liked this · 2 years ago
ring-theory liked this · 2 years ago -
 eos-exp liked this · 2 years ago
eos-exp liked this · 2 years ago -
 germax26 liked this · 2 years ago
germax26 liked this · 2 years ago -
 tiedbyagoldennecklace liked this · 2 years ago
tiedbyagoldennecklace liked this · 2 years ago -
 infernal-heart reblogged this · 2 years ago
infernal-heart reblogged this · 2 years ago -
 infernal-heart liked this · 2 years ago
infernal-heart liked this · 2 years ago -
 maeve-the-platemail-butch liked this · 2 years ago
maeve-the-platemail-butch liked this · 2 years ago -
 hacvek liked this · 2 years ago
hacvek liked this · 2 years ago -
 mathamatacs reblogged this · 2 years ago
mathamatacs reblogged this · 2 years ago -
 fysyx liked this · 2 years ago
fysyx liked this · 2 years ago -
 fysyx reblogged this · 2 years ago
fysyx reblogged this · 2 years ago -
 ips-n-caliban liked this · 2 years ago
ips-n-caliban liked this · 2 years ago -
 raloxifiend liked this · 2 years ago
raloxifiend liked this · 2 years ago -
 wasabipesto liked this · 2 years ago
wasabipesto liked this · 2 years ago -
 gxngarr liked this · 2 years ago
gxngarr liked this · 2 years ago -
 heavenlyhorses liked this · 2 years ago
heavenlyhorses liked this · 2 years ago -
 parmacotto reblogged this · 2 years ago
parmacotto reblogged this · 2 years ago -
 parmacotto liked this · 2 years ago
parmacotto liked this · 2 years ago -
 transgenderer reblogged this · 2 years ago
transgenderer reblogged this · 2 years ago -
 hallasurvivor reblogged this · 2 years ago
hallasurvivor reblogged this · 2 years ago

⁕ pure math undergrad ⁕ in love with anything algebraic ⁕
292 posts
