13 X 2022

me when Čech cohomology

i love math. i hate math. i can do it all day, everyday. i cannot solve a single question. it's my favorite subject. I would rather kms than open the book. it's beautiful and everything makes sense and it's the best. it's fucking useless and nothing is logical and it's the worst. it's the loml. it's my arch nemesis.

Venn diagrams that have a number of sets that AREN'T prime numbers (except 1, but it's trivial) cannot be rotationally symmetrical, so here are a couple real 6-set venn diagrams.

Someone PLEASE use one of these to make a diagram. I'm begging. i need to see it with my own eyes.

I have a bet going on with a friend. We need a third opinion. Can one find the square root of 2 in pi? And pi in the root of 2

Gut instinct says no. But when you work with infinities, gut instinct is NOT proof. (And such a gut feeling could have easily been the dodgy dinner I cooked myself last night.)

However I cannot even provide a proof.

I have, however tried to give some insight in another post (it should be the one immediately below this one) to perhaps help/provoke a more concrete argument from someone else :)

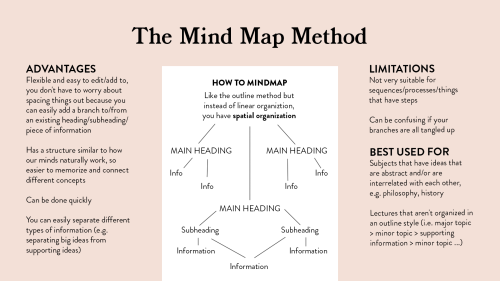
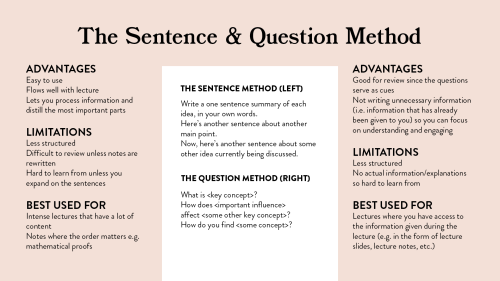
An Overview of Note-Taking Styles

Note-taking is one of the most essential skills a student should master. It allows you to record and review information to be used in the future. But what’s the best way to do so? Here’s an overview of note-taking styles that can help you maximize your learning!

8 V 2022

I am on my way home from a math conference, the first one in which I participated actively – I prepaired the talk about the Borsuk-Ulam theorem

my lecture was centered around the connection between the classic "continuous" BUT and its combinatorial analog: Tucker's lemma

I wanted to talk about this because I was amazed at how cool and "versatile" this theorem is. there is a whole book about its applications and generalizations, which is btw very well-written, I highly encourage everyone to read it:

my presentation went well, although after practicing it for about a week the topic seemed really fucking boring to me, no wonder

other than that I have another recommendation to make. do you also hate how messy multivariable calculus is? I do. calculations and technical definitions everywhere, and at the end everything comes down to calculating the determinant of some jacobian. bluh. I stumbled upon a book that describes everything from a sort of algebraic perspective, smells a little bit like category theory too. very clean, very satisfying to read:

I have been studying covering spaces recently and I can give some dope motivation for learning about the structure induced by the covering mapping:

I will never forget that the homomorphism induced by the covering projection is injective

that would be it for my mathemathical life. my personal life, which is still closely connected to math, brings me some psychological progress. I no longer get stuck in loops of "oh I'm so bad at math. maybe I'm not? I got a good grade from X. ah but I got a shit grade afterwards". it might be because I didn't fall on my face for a while now, only decent grades, good ideas, a good presentation, this is correct. but I also do not negotiate with myself that this is supposed to be proof that I'm good enough, I just stopped paying attention to these and focused on math instead. and paradoxically when I stopped caring about being good at math I was rewarded with getting better at math???

a coincidence,

a pleasant one, nonetheless.

anyway I will have to take a fall at some point, unavoidable. and it will be the final test of my progress, becauase I used to get very elevated in my sense of self-worth after receiving a single good grade among trash ones and now I'm just ok. not the god, just ok. but back then, at some point I would no longer be god, I would get smacked in the face by some "proof that I'm actually trash" and that would be a fall from a significant altitude. so I'm hoping that the fall will also be less painful now

I think the biggest change I made was giving up, I abandoned all hope. nooow here is the moment when people interrupt me with "nooo that's horrible don't give up you're a great person you just have to notice that"

fuck off you don't understand shit

I'm doing better now precisely because I stopped hoping that one day I'll stop feeling worthless, that one day something great will happen that will prove once and for all that I'm meant for something great. I can't stand this anymore, I am disgusted by the fact that deep down I still believe that I'm supposed to be the best and that I can't enjoy anything unless I am winning. I want to puke when I'm reminded that everything I do serves the purpose of winning the negotiations I have with myself about what my actual value is

my self-hatred runs much deeper now than ever before and I have no more patience for self-victimization, no more room for "allowing myself to feel". fuck off, all I feel is rage. I want to be able to do things without the prospect of a reward, my goal is to enjoy things, not the sense of being good at doing things

so that's what I'm doing, I made peace with the fact that I will probably never feel good about myself and that I have no chance at achieving the greatness I crave. and I must say I started respecting myself more, turns out I am actually able to do things without the promise of being the best at them, the vision of bringing value to the world motivates me. and fuck the western culture with its oh you must love yourself you are a great person. no, you don't have to do that and you have no way of knowing what kind of person you are, nobody has ever defined it in a strict formal sense, people just use this phrase to trigger the feel-good in others

I am aware that all of this sounds really bad, but I don't care, it works. and my math will be better like that because now that I stopped crying over being trash I have more time to study

I just hope that the fall won't be as painful

yeah I say that I'm vegetarian because the texture of meat fucks with my sensory issues. I would know if the meat in my meal was real and I would probably throw up and have a meltdown, then proceed to have my day ruined. I can't believe someone actually could put me in such a position jfc

Look I clown veganism often enough but really, truly, don’t ever fucking feed somebody something without their knowledge or consent. It’s hugely fucked up and not OK.

good point! I should add to my list the golden rule of asking yourself "does this thing that I'm currently trying actually work for me". in the meantine I had a conversation with a friend who said that for her not caring about the aesthetics of notes decreases the effectiveness of studying, my perspective definitely isn't The Only Correct One

the best method is the one that works. it's perfectly okay to benefit from notes, from making them pretty, it's also perfectly okay to limit the notes. it was a surprising discovery for me that taking notes doesn't help with my learning, because my whole life I've been told to always take notes. but of course this isn't going to work for everyone, thank you for pointing this out

tips for studying math

I thought I could share what I learned about studying math so far. it will be very subjective with no scientific sources, pure personal experience, hence one shouldn't expect all of this to work, I merely hope to give some ideas

1. note taking

some time ago I stopped caring about making my notes pretty and it was a great decision – they are supposed to be useful. moreover, I try to write as little as possible. this way my notes contain only crucial information and I might actually use them later because finding things becomes much easier. there is no point in writing down everything, a lot of the time it suffices to know where to find things in the textbook later. also, I noticed that taking notes doesn't actually help me remember, I use it to process information that I'm reading, and if I write down too many details it becomes very chaotic. when I'm trying to process as much as possible in the spot while reading I'm better at structuring the information. so my suggestion would be to stop caring about the aesthetics and try to write down only what is the most important (such as definitions, statements of theorems, useful facts)

2. active learning

do not write down the proof as is, instead write down general steps and then try to fill in the details. it would be perfect to prove everything from scratch, but that's rarely realistic, especially when the exam is in a few days. breaking the proof down into steps and describing the general idea of each step naturally raises questions such as "why is this part important, what is the goal of this calculation, how to describe this reasoning in one sentence, what are we actually doing here". sometimes it's possible to give the proof purely in words, that's also a good idea. it's also much more engaging and creative than passively writing things down. another thing that makes learning more active is trying to come up with examples for the definitions

3. exercises

many textbooks give exercises between definitions and theorem, doing them right away is generally a good idea, that's another way to make studying more active. I also like to take a look at the exercises at the end of the chapter (if that's the case) once in a while to see which ones I could do with what I already learned and try to do them. sometimes it's really hard to solve problems freshly after studying the theory and that's what worked out examples are for, it helps. mamy textbooks offer solutions of exercises, I like to compare the "official" ones with mine. it's obviously better than reading the solution before solving the problem on my own, but when I'm stuck for a long time I check if my idea for the solution at least makes sense. if it's similar to the solution from the book then I know I should just keep going

4. textbooks and other sources

finding the right book is so important. I don't even want to think about all the time I wasted trying to work with a book that just wasn't it. when I need a textbook for something I google "best textbooks for [topic]" and usually there is already a discussion on MSE where people recommend sources and explain why they think that source is a good one, which also gives the idea of how it's written and what to expect. a lot of professors share their lecture/class notes online, which contain user-friendly explenations, examples, exercises chosen by experienced teachers to do in their class, sometimes you can even find exercises with solutions. using the internet is such an important skill

5. studying for exams

do not study the material in a linear order, instead do it by layers. skim everything to get the general idea of which topics need the most work, which can be skipped, then study by priority. other than that it's usually better to know the sketch of every proof than to know a half of them in great detail and the rest not at all. it's similar when it comes to practice problems, do not spend half of your time on easy stuff that could easily be skipped, it's better to practice a bit of everything than to be an expert in half of the topics and unable to solve easy problems from the rest. if the past papers are available they can be a good tool to take a "mock exam" after studying for some time, it gives an opoortunity to see, again, which topics need the most work

6. examples and counterexamples

there are those theorems with statements that take up half of the page because there are just so many assumptions. finding counterexamples for each assumption usually helps with that. when I have a lot of definitions to learn, thinking of examples for them makes everything more specific therefore easier to remember

7. motivation

and by that I mean motivation of concepts. learning something new is much easier if it's motivated with an interesting example, a question, or application. it's easier to learn something when I know that it will be useful later, it's worth it to try to make things more interesting

8. studying for exams vs studying longterm

oftentimes it is the case that the exam itself requires learning some specific types of problems, which do not really matter in the long run. of course, preparing for exams is important, but keep in mind that what really matters is learning things that will be useful in the future especially when they are relevant to the field of choice. just because "this will not be on the test" doesn't always mean it can be skipped

ok I think that's all I have for now. I hope someone will find these helpful and feel free to share yours

Mathematics: What do grad students in math do all day?

Mathematics: What do grad students in math do all day? - gist:4158578

“A lot of math grad school is reading books and papers and trying to understand what’s going on. The difficulty is that reading math is not like reading a mystery thriller, and it’s not even like reading a history book or a New York Times article.

The main issue is that, by the time you get to the frontiers of math, the words to describe the concepts don’t really exist yet. Communicating these ideas is a bit like trying to explain a vacuum cleaner to someone who has never seen one, except you’re only allowed to use words that are four letters long or shorter.

What can you say?

“It is a tool that does suck up dust to make what you walk on in a home tidy.”

That’s certainly better than nothing, but it doesn’t tell you everything you might want to know about a vacuum cleaner. Can you use a vacuum cleaner to clean bookshelves? Can you use a vacuum cleaner to clean a cat? Can you use a vacuum cleaner to clean the outdoors?

The authors of the papers and books are trying to communicate what they’ve understood as best they can under these restrictions, and it’s certainly better than nothing, but if you’re going to have to work with vacuum cleaners, you need to know much more.

Fortunately, math has an incredibly powerful tool that helps bridge the gap. Namely, when we come up with concepts, we also come up with very explicit symbols and notation, along with logical rules for manipulating them. It’s a bit like being handed the technical specifications and diagrams for building a vacuum cleaner out of parts.

The upside is that now you (in theory) can know 100% unambiguously what a vacuum cleaner can or cannot do. The downside is that you still have no clue what the pieces are for or why they are arranged the way they are, except for the cryptic sentence, “It is a tool that does suck up dust to make what you walk on in a home tidy.”

OK, so now you’re a grad student, and your advisor gives you an important paper in the field to read: “A Tool that does Suck Dust.” The introduction tells you that “It is a tool that does suck up dust to make what you walk on in a home tidy,” and a bunch of other reasonable but vague things. The bulk of the paper is technical diagrams and descriptions of a vacuum cleaner. Then there are some references: “How to use air flow to suck up dust.” “How to use many a coil of wire to make a fan spin very fast.” “What you get from the hole in the wall that has wire in it.”

So, what do you do? Technically, you sit at your desk and think. But it’s not that simple. First, you’re like, lol, that title almost sounds like it could be sexual innuendo. Then you read the introduction, which pleasantly tells you what things are generally about, but is completely vague about the important details.

Then you get to the technical diagrams and are totally confused, but you work through them piece by piece. You redo many of the calculations on your own just to double check that you’ve really understood what’s going on. Sometimes, the calculations that you redo come up with something stupid, and then you have to figure out what you’ve understood incorrectly, and then reread that part of the technical manual to figure things out. Except sometimes there was a typo in the paper, so that’s what screwed things up for you.

After a while, things finally click, and you finally understand what a vacuum cleaner is. In fact, you actually know much more: You’ve now become one of the experts on vacuum cleaners, or at least on this particular kind of vacuum cleaner, and you know a good fraction of the details on how it works. You’re feeling pretty proud of yourself, even though you’re still a far shot from your advisor: They understand all sorts of other kinds of vacuum cleaners, even Roombas, and, in addition to their work on vacuum cleaners, they’re also working on a related but completely different project about air conditioning systems.

You are filled with joy that you can finally talk on par with your advisor, at least on this topic, but there is a looming dark cloud on the horizon: You still need to write a thesis.

So, you think about new things that you can do with vacuum cleaners. So, first, you’re like: I can use a vacuum cleaner to clean bookshelves! That’d be super-useful! But then you do a Google Scholar search and it turns out that someone else did that like ten years ago.

OK, your next idea: I can use a vacuum cleaner to clean cats! That’d also be super-useful. But, alas, a bit more searching in the literature reveals that someone tried that, too, but they didn’t get good results. You’re a confident young grad student, so you decide that, armed with some additional techniques that you happen to know, you might fix the problems that the other researcher had and get vacuuming cats to work. You spend several months on it, but, alas, it doesn’t get you any further.

OK, so then, after more thinking and doing some research on extension cords, you think it would be feasible to use a vacuum cleaner to clean the outdoors. You look in the literature, and it turns out that nobody’s ever thought of doing that! You proudly tell this idea to your advisor, but they do some back of the envelope calculations that you don’t really understand and tell you that vacuuming the outdoors is unlikely to be very useful. Something about how a vacuum cleaner is too small to handle the outdoors and that we already know about other tools that are much better equipped for cleaning streets and such.

This goes on for several years, and finally you write a thesis about how if you turn a vacuum cleaner upside-down and submerge the top end in water, you can make bubbles!

Your thesis committee is unsure of how this could ever be useful, but it seems pretty cool and bubbles are pretty, so they think that maybe something useful could come out of it eventually. Maybe.

And, indeed, you are lucky! After a hundred years or so, your idea (along with a bunch of other ideas) leads to the development of aquarium air pumps, an essential tool in the rapidly growing field of research on artificial goldfish habitats. Yay!”