→ 25 VIII 2021

Want to learn something new in 2022??

Absolute beginner adult ballet series (fabulous beginning teacher)

40 piano lessons for beginners (some of the best explanations for piano I’ve ever seen)

Excellent basic crochet video series

Basic knitting (probably the best how to knit video out there)

Pre-Free Figure Skate Levels A-D guides and practice activities (each video builds up with exercises to the actual moves!)

How to draw character faces video (very funny, surprisingly instructive?)

Another drawing character faces video

Literally my favorite art pose hack

Tutorial of how to make a whole ass Stardew Valley esque farming game in Gamemaker Studios 2??

Introduction to flying small aircrafts

French/Dutch/Fishtail braiding

Playing the guitar for beginners (well paced and excellent instructor)

Playing the violin for beginners (really good practical tips mixed in)

Color theory in digital art (not of the children’s hospital variety)

Retake classes you hated but now there’s zero stakes:

Calculus 1 (full semester class)

Learn basic statistics (free textbook)

Introduction to college physics (free textbook)

Introduction to accounting (free textbook)

Learn a language:

Ancient Greek

Latin

Spanish

German

Japanese (grammar guide) (for dummies)

French

Russian (pretty good cyrillic guide!)

Artificial intelligence makes accurate sheep counting.

Person: *breathes*

Graph Theorists: NO NOT THAT KIND OF GRAPH

I know your thesis was about something to do with algebraic topology, may I ask what exactly it was about?

(and congrats to you getting your bachelors degree and into a masters program)

(thank you!)

my thesis was about an open question regarding a certain skein module of tangles on 2n nodes. the conjecture is that the module is free and in my thesis I constructed a generating set that is free for n=2,3 (direct calculation) but I have yet to prove that for a general n. if you are interested I can send you the paper in which the question was posed, all the details are explained there and would be hard to write down here without tex lol

yes, this. taking photos of the blackboard and writing down only the "sketch" of the lecture usually does the trick for me: I have all the details I need but I'm able to actually listen

a thing that i didn’t understand as a student, that many of my students don’t understand, and that i still sometimes struggle to put into practice: taking the most detailed notes is not always the best way to learn the material. trying to write down every single thing a teacher (or other person who is presenting auditory information to you) says is not only slow but it also can easily stop you from being mentally present during the lesson, internalizing the main ideas and how everything fits together, which is what will actually help you learn the material.

hairy ball theorem, stokes theorem, poincaré duality, nullstellensatz, idk too much to choose one

What is your favourite mathematical theorem? I'm personally torn between the compactness theorem for first-order logic, and the fundamental theorem of Galois theory.

http://proof.ucalgaryblogs.ca/

This is the best resource for studying math that I've found in a while! It's 300+ pages of flawed/incorrect proofs on topics including logic, analysis, and linear algebra. Each flawed proof is followed by a classification of its errors, and a corrected version.

refseek.com

www.worldcat.org/

link.springer.com

http://bioline.org.br/

repec.org

science.gov

pdfdrive.com

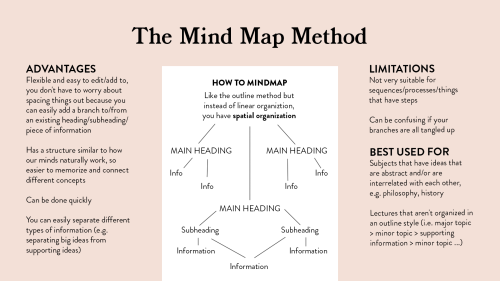
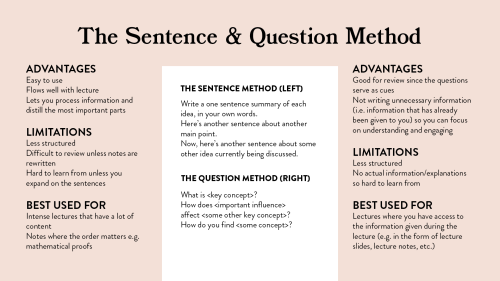
An Overview of Note-Taking Styles

Note-taking is one of the most essential skills a student should master. It allows you to record and review information to be used in the future. But what’s the best way to do so? Here’s an overview of note-taking styles that can help you maximize your learning!

7 III 2023

it's the second week of the semester and I must say that it's easier than I predicted

statistical data analysis is boring but easy, algebra 2 is easy but probably interesting, so is differential geometry

algebraic topology was funny because ⅓ of the group completed the algebraic methods course, so at first we told the professor to skip half of the lecture (we all know the required part of category theory) and then with every new piece of information he would say "ok maybe this will be the first thing today that you don't know", to which we would reply "naaah we've seen this" lmao. but the course overall will be fun and maybe it's even better that the level of difficulty won't be as high as I though, that would leave more time for my other stuff

the tutorial part of number theory was scary, because the professor wanted us to work in pairs. my autistic ass hates working in groups and the noise in the room was unbearable (everyone was talking about the exercises we were given to solve), so I was on the verge of a meltdown after 30 minutes of this despite ANC headphones. next time I will work by myself from the start. maybe without the requirement of communication it won't be as bad. the course itself will be easy, when it comes to the material. I know nothing about number theory, so the novelty will make it more enjoyable. a few people said that they would prefer the tutorial in the standard form, maybe I won't have to worry about surviving it if there are enough people who want to change it

my birthday is tomorrow and as a gift my parents gave me enough money to buy an ipad, I was saving for it since november. for a few days now I've been testing different apps for note taking, pdf readers and other tools useful for studying. I must say, this is a game changer, I absolutely love it

taking notes itself is less comfortable than on an e-ink tablet, which gives very paperlike experience, but it's better than traditional ones. the upside is that I can use different colors and the whole process is less rigid than on an e-ink

two apps that seem the best for now are MarginNote 3 and GoodNotes

the first one is good for studying something from multiple sources. the app allows to open many pdfs, take pieces from them and then arrange them in a mindmap. it's possible to add handwritten notes, typed notes, photos and probably more that I don't know yet. all of this seems to be particularly useful when studying for exams or in other situations when it's necessary to review a huge chunk of material

the second app is for regular handwritten notes. it doesn't have any special advantages other than I just like the interface lol what I like about taking notes on ipad is that I can take photos and insert them directly into the notebook, which I can't do on the e-ink. it's great for lectures and classes because I don't usually write everything down (otherwise I can't listen, too busy with writing) and even if I do, I don't trust myself with it so I take photos anyway. being able to merge the photos with notes reduces chaos

oh god this is going to be a long post! other news from life is that yesterday I had a meeting with my thesis advisor and we finally picked a topic. some time ago he sent me a paper to try and said, very mysteriously, to let him know if it's not too hard before he reveals more details about his idea. the paper is about symmetric bilinear forms on finite abelian groups, pure algebra, and I was supposed to write about algebraic topology, so I tried to search where this topics comes up, but didn't find anything. it turns out that it's used to define some knot invariant, which I would use to write about the classification of singularities of algebraic curves. in the meantime my advisor had another idea, which is an open problem in knot theory. we decided to try the second one, because there is less theory to learn before I could start writing the paper

to summarize what I'm about to do: there is a knot invariant called Jones polynomial, which then inspires a construction of a certain R-module on tangles and the question asks whether that module is free, if so, what is its rank. now I'm reading the book he gave me to learn the basics and I can't wait till I start working on the problem