Embryo Geometry: A Theory Of Evolution From A Single Cell To The Complex Vertebrate Body

Embryo geometry: a theory of evolution from a single cell to the complex vertebrate body

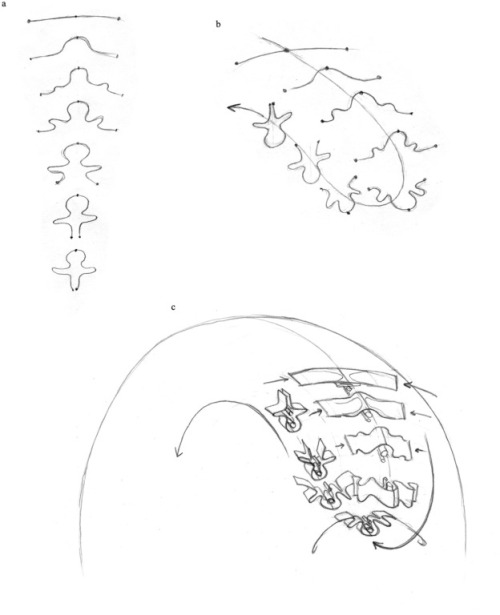
24 “blueprints” that illustrate how the musculoskeletal, cardiovascular, neurological, and reproductive systems evolve through the mechanical deformation of geometric patterns. These images show how the vertebrate body might have evolved from a single cell during the evolutionary time and during individual development.

Though neither rigorous nor exhaustive in an empirical sense, our model offers an intuitive and plausible description of the emergence of form via simple geometrical and mechanical forces and constraints. The model provides a template, or roadmap, for further investigation, subject to confirmation (or refutation) by interested researchers.

The concept of “embryo geometry” suggests that the vertebrate embryo might be produced by mechanical deformation of the blastula, a ball of cells formed when a fertilized egg splits. As these cells multiply, the volume and surface area of the ball expand, changing its shape. According to the hypothesis, the blastula preserves the geometry of the initial eight cells generated by the egg’s first three divisions, which establish the three axes of the vertebrate body.

Though speculative, the model addresses the poignant absence in the literature of any plausible account of the origin of vertebrate morphology. A robust solution to the problem of morphogenesis—currently an elusive goal—will only emerge from consideration of both top-down (e.g., the mechanical constraints and geometric properties considered here) and bottom-up (e.g., molecular and mechano-chemical) influences.

Origin of the vertebrate body plan via mechanically biased conservation of regular geometrical patterns in the structure of the blastula, David B. Edelman, Mark McMenamin, Peter Sheesley, Stuart Pivar

Published: September 2016, Progress in Biophysics and Molecular Biology DOI: 10.1016/j.pbiomolbio.2016.06.007