Throughout History, The Wealthy And Powerful Tend To Create A Set Of Rules For Themselves To Follow-

I guess I ahould probably start doing things

Gluttonous wunk

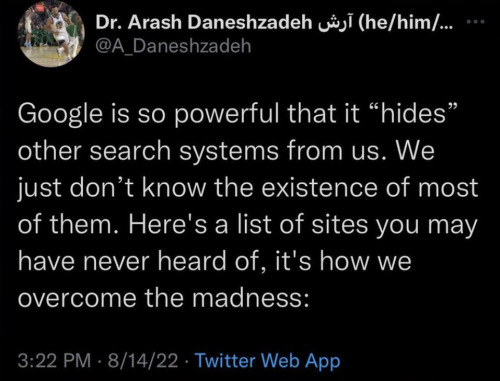
refseek.com

www.worldcat.org/

link.springer.com

http://bioline.org.br/

repec.org

science.gov

pdfdrive.com

you ever heard a lightning fucking scream?

youre about to

i love making art

you've probably answered this already but what are some good shoegaze albums to liste to if i wated to check out the genre?

OOOH GREAT QUESTION!!! definitely ceres and calypso in the deep time by candy claws but also daydream twins and lucid express self titleds and a fusion of two hemispheres by sphere and loveless by my bloody valentine and ill leave you with those for now :)!!!!

There he go

gummy lamas

P(A)=Number of favorable outcomesTotal number of possible outcomesP(A) = \frac{\text{Number of favorable outcomes}}{\text{Total number of possible outcomes}}P(A)=Total number of possible outcomesNumber of favorable outcomes​

P(A′)=1−P(A)P(A') = 1 - P(A)P(A′)=1−P(A)

P(A∪B)=P(A)+P(B)P(A \cup B) = P(A) + P(B)P(A∪B)=P(A)+P(B)

P(A∪B)=P(A)+P(B)−P(A∩B)P(A \cup B) = P(A) + P(B) - P(A \cap B)P(A∪B)=P(A)+P(B)−P(A∩B)

P(A∣B)=P(A∩B)P(B)P(A | B) = \frac{P(A \cap B)}{P(B)}P(A∣B)=P(B)P(A∩B)​

P(A∩B)=P(A)⋅P(B)P(A \cap B) = P(A) \cdot P(B)P(A∩B)=P(A)⋅P(B)

P(A∩B)=P(A)⋅P(B∣A)P(A \cap B) = P(A) \cdot P(B | A)P(A∩B)=P(A)⋅P(B∣A)

P(A∣B)=P(B∣A)⋅P(A)P(B)P(A | B) = \frac{P(B | A) \cdot P(A)}{P(B)}P(A∣B)=P(B)P(B∣A)⋅P(A)​

P(A)=∑i=1nP(A∣Bi)⋅P(Bi)P(A) = \sum_{i=1}^{n} P(A | B_i) \cdot P(B_i)P(A)=∑i=1n​P(A∣Bi​)⋅P(Bi​)

p(x)p(x)p(x): E(X)=∑xx⋅p(x)E(X) = \sum_{x} x \cdot p(x)E(X)=∑x​x⋅p(x)

Var(X)=E(X2)−[E(X)]2\text{Var}(X) = E(X^2) - [E(X)]^2Var(X)=E(X2)−[E(X)]2

σX=Var(X)\sigma_X = \sqrt{\text{Var}(X)}σX​=Var(X)​

P(X=k)=(nk)pk(1−p)n−kP(X = k) = \binom{n}{k} p^k (1-p)^{n-k}P(X=k)=(kn​)pk(1−p)n−k where (nk)=n!k!(n−k)!\binom{n}{k} = \frac{n!}{k!(n-k)!}(kn​)=k!(n−k)!n!​

P(X=k)=λke−λk!P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}P(X=k)=k!λke−λ​

f(x)=1σ2πe−(x−μ)22σ2f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}f(x)=σ2π​1​e−2σ2(x−μ)2​