Meanwhile Typical Conversations Between My Friends:

but how is this related to adhd? I'd say my ability to have fun is diminished because of the dopamine deficiency, I'm basically constantly bored, and afaik adhd increases the risk of substance abuse disorders, so I don't see the point of bringing up adhd in this context

Me: I don't take alcohol, smoke weed or do any other substances.

Everyone: Omg!! then how do you have fun??

Me: I have ADHD.

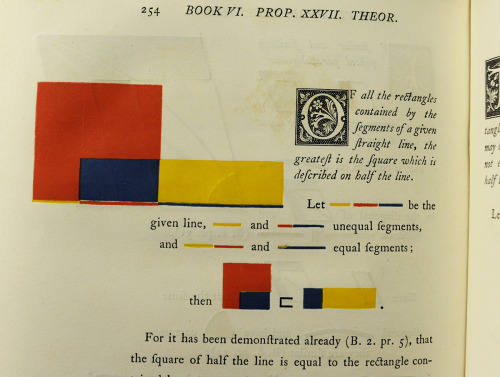
The beautiful modernism of Oliver Byrne’s, The First Six Books of the Elements of Euclid, 1847

that's an interesting perspective

recently I've been thinking about it in an opposite way. it started during a conversation about brains, in particular how stupid and flawed they are, I realized that I enjoy math because it gives me a break from being human. there is no place for emotion and cognitive bias, only formal reasoning and proofs. it feels so safe and so distant from the day-to-day life filled with problems caused by the human nature, it feels so clean. it's a place for me to enjoy only the best qualities of my existence. it's an acceptable way to separate myself from everyone, and simultaneously stay connected

I love how different this is from what is described above, as if math offered a place for everyone to find something that they will like

Im trying to find a really long Tumblr post that talked about how sad it was that people are so happy to complain about how much they hated math and how math can be a way to connect with your fundamental humanity and...

Yeah, I've been studying a little bit of it on my own, ten years after I dropped out of college, I've been going back to seeing some basics of calculus, and I've been really feeling some of that.

There is this sense that math is this alien thing, separate from the true concerns of humanity. This external topic, strange and inhumane that only those few weirdos with a eccentric and atypical cast of mind, who are themselves separate by a few degrees from human nature, can grasp.

But it's not that, We, messy warm emotional dumb humans came up with it, we silly atavistic creatures dedicated so much time and effort to develop it and explore it, this silly, quirky, wet, ape-like species is the only living creature on this planet that concerns itself with doing math in any serious capacity. It didn't come from aliens or the gods or from dolphins, math came from humans and humans are the only ones that use them. There could be nothing more human, more fundamentally ours, more intrinsic to our nature than math.

And it's not just a tool! Is not just this thing to be celebrated because its useful in a purely base pragmatical, prosaic way. Is not this thing we have to dissapasionatly conceed credit to because I guess it does useful things like bridges and rockets and computers and taxes. Math is not just the civilizational equivalent of going to the dentist or eating your vegetables.

i hesitate to call it a philosophy or an art, it is a way of human thinking, it is a way of thinking like a human, of thinking in a way that only humans can think. its is one of our oldest and proudest traditions, it is a way to feel greater than onself, it is a way of growing. it is a song with a prosody all its own. There is such a profound sense of meaning and beauty and truth and purpose to be found in math, and the best of all is that it works, when it says something it means something, its telling you a thing that is meaningful, that represents something true, that couldnt be any other way, that has consequences and uses and can be relied upon, that it representes something which carries weight and its ours, its truly a part of our nature, of what we are.

Pick a point inside a triangle and drop perpendicular projections onto the sides. These define another triangle. Repeat, with the same point but within the new triangle. Do the same thing once more. The fourth triangle now has the same angles as the first one, although it’s much smaller and it’s rotated.

just had a reflection about perfectionism. today I had an exam for which I was prepared very well, but my stupid brain happened and I didn't get the highest grade. my boyfriend was comforting me and he asked since when I want to ace everything, this question made me think

indeed, I don't want to ace everything. I am taking 4 courses this semester, one of which I don't care about enough to strive for the best grade, one of which is way too hard to aim that far, two of which I thought were achievable. and now I didn't achieve that. it feels different to set unrealistic goals and then never achieve them than to set very realistic ones and still fail, that's what I realized today

I am not a perfectionist. I used to be, years ago, and then I learned to set realistic goals. now I'm thinking, isn't perfectionism a kind of a coping mechanism? deep down you know your goals are impossible, so it's not really surprising when you fail. you are never satisfied, sure, but maybe it does feel more safe this way than to not know if you will be satisfied or disappointed. if that's the case then setting realistic goals is absolutely not the way to heal perfectionism

imo euclidean geometry kinda sucks, but if we mean geometry in a more general sense then algebraic geometry is the one

I've decided to start a fight

anyways geometry sucks algebra best math

I have a possibly unusual question. since I left high school and was no longer being forced to read I completely stopped looking at fiction and other books that are not math textbooks. this is partly because I fucking hated reading as an activity – I have adhd and asd, so not only my attention regulation causes a lot of problems, I also struggle with visualizing what's happening and imagining/undestanding the intentions and mindsets of the characters. now, I am properly medicated so attention isn't as much of an issue anymore and I remember enjoying some of the books I've been forced to go through. I miss reading, overall it had a positive impact on my thinking process, I miss analyzing the human experience, so to speak

I liked Dostoyevsky, Vonnegut, Philip K. Dick, Huxley, Kafka and some other "philosophified" authors. I also enjoyed war-themed books in general such as all quiet on the western front, and everything related to the soviet union

finally, my question is, what would you recommend for someone with this taste, who also likes math¹, has a hard time with visual imagination and people but enjoys analyzing human experience, who would possibly like to see a represenation of themselves in the characters of the novel? I would love to rebuild my reading habits, but I am lost as to where to start so I don't get discouraged

¹ I included math in here because maybe there is a book about what it's like to be a mathematician (or a scientist of some kind) that give some existentialist vibes or something, if it exists I want to read it lol

september

I decided to start posting monthly, I hope it will help me keep it regular during the semester, it may also bring more structure into my posts

I gave my talk at the conference, I was surprised with the engagement I received, people asked a lot of questions even after the lecture was over. it seemed to be very successful in a sense that so many people found the topic interesting

what I need to do the most in the next 3 weeks is learn the damn geometry. sometimes I take breaks to study algebraic tolology, I did that yesterday

you guys seem to enjoy homology so here is me computing the simplicial homology groups of the projective plane. I tried to take one of these aesthetic photos I sometimes see on other studyblrs but unfortunately this is the best I can do lmao

my idea for mainly reading and taking notes only when it's for something really complicated seems to be working. I focus especially on the problem-solving side of things, because as I learned the hard way, I need to learn the theory and problem-solving separately. what I found is that sitting down and genuinely trying to prove the theorems stated in the textbook is a good way to get a grasp of how the problems related to that topic are generally treated. sometimes making one's own proof is too difficult, well, no wonder, experienced mathematicians spend months trying to get the result, so why would I expect myself to do that in one sitting. then I try to put a lot of effort into reading the proof, so that later I can at least describe how it's done. I find this quite effective when it comes to learning a particular subject. I will never skip the proof again lmao

in a month I'll try to post about the main things I will have managed to do, what I learned, what I solved, and hopefully more art projects

maybe a littel late for Real’s Math Ask Meme 18, 6 and 3, please?

hi, thanks for the questions!

3: what math classes did you like the most?

tough choice! for the content itself I'd say abstract algebra, commutative algebra, analytic functions and algebraic topology. for the way the class was taught, a course on galois theory I took last semester was probably the best. the pace of the lecture allowed me to learn everything on the spot, not too fast, but not so slow that my mind would wander. the tutorials were also great, because the teacher found the perfect balance between explaining and showing the solutions, and engaging us to think about what should happen next. the courses I mentioned above were also taught well, but the galois theory one was absolutely perfect

6: why do you learn math?

I enjoy the feeling of math in my brain. I can spend hours thinking about a problem and not get bored, which doesn't usually happen with other things. when I finish a study session I feel tired in a good way, like I spent my time and energy doing something valuable and it's very satisfying

18: can you share a good math problem you've solved recently?

given a holomorphic line bundle L over a compact complex manifold, prove that L is trivial iff L and the dual of L both admit a non-zero section

this problem is quite basic, in a sense that you work on it right after getting started with line bundles, but I believe it to be a good problem, because it forces you to analyze the difference between trivial holomorphic bundles and trivial smooth bundles, so it's great for building some intuition

25 II 2023

I had an exam yesterday, one more to go. it was the written part, so 12+ hours of solving problems, exhausting just like before. I completed all of them, but of course I am not sure if my solutions are correct, I will find out on monday. I'm proud of the progress I've made

right now I'm studying for the second part, so the theory-oriented one, I can barely focus because I've already learned those things and now I have to relearn them again

I'm trying to prove all the theorems on my own. partly to see how much I remember, partly to see how much I'm willing to improvize. as they say, if you're using too much memory then you're doing something wrong so I'm hoping to be able to come up with the proofs without memorizing anything new

my technique for studying the theory for the exam is to first test myself on how much I remember by trying to write everything down and note where I'm unsure or don't remember at all. then I read the textbooks starting from the worst topics up to the better ones. when I encounter a long complicated proof I am trying to break it down into steps and give each step a "title" or a short description

for instance, the Baer criterion featured in the photo has the following steps:

only do "extenstions on ideals to R→M ⇒ M injective"

define the poset of extenstions of A → M, A ⊆ B and a contrario suppose there is a maximal element ≠B

use the assumption to define an ideal and a submodule that contradicts the maximality of the extension

it is much easier to fill out the details than to remember the whole thing. this is probably the biggest skill I acquired this semester, next to downloading lecture notes pdfs of random professors I find online lmao

a friend suggested that I could make a post about tips for reading math textbooks and papers. as for papers, I don't have enough experience to give any tips, but I can share how I approach reading the books

a big news in my life is that I got a job. I will be a programmer and I start in march. at first I am going to use mostly python, but in the long run they will have me learn java. I'm excited and terrified at the same time, this semester is gonna kill me