Bsdndprplplld - You Can't Comb A Hairy Ball

30 VII 2021

did some stuff today. found out my cat would die tomorrow if it wasn't for an operation he had today, that didn't feel good but also oh god was he lucky

sleep: better but still trash. yesterday fell asleep between 3 and 4, today planning to go to bed at 3 so in a few minutes

concentration: not as great. couldn't focus because my cat was fucking dying

bo phone time: decent

did some topo today, i think i managed to understand the idea behind the quotient spaces and i really liked it. can't wait to dive deeper tomorrow. other than that i wrote a method that takes a parametric function and provides a partition dividing the curve into k intervals. also i'm almost done with the art comission

sooo tomorrow i plan to finish the code, i want to achieve the functionality that takes a parametric function and draws it with a dashed line. that's why i needed the partition, it's gonna look fucking beautiful. and i need to complete the comission. i hope there will be some time left for quotient spaces, i am very hyped. oh and i forgot i'm drinking tomorrow. so i guess no topo for that gal. eh

Venn diagrams that have a number of sets that AREN'T prime numbers (except 1, but it's trivial) cannot be rotationally symmetrical, so here are a couple real 6-set venn diagrams.

Someone PLEASE use one of these to make a diagram. I'm begging. i need to see it with my own eyes.

today I learned that for a surface with boundary, which I believe we can say a straw is, the genus is equal to that of a 2-manifold obtained from attaching disks to the boundary. hence the straw has genus equal to that of a 2-sphere, which is 0, therefore a straw has 0 holes

also a straw is not homotopic to a torus I think, but rather to S¹, as it's a product of S¹ and a closed interval, which is contractible. a torus has the fundamental group S¹×S¹, thus they cannot be homotopy equivalent. buuut that requires the straw to be infinitely thin so maybe I'm too idealistic for this claim to hold and it is in fact equivalent to a torus

lmao I love math but I can't stop laughing at the fact that it took me two years of university to be able to have this discussion

I’m really into internet discourse but only pointless and stupid internet discourse like how many holes there are in a straw (it’s 2)

Thank you, /r/ProgrammerHumor, I love you endlessly.

Redditors competing to make the worst volume sliders possible...

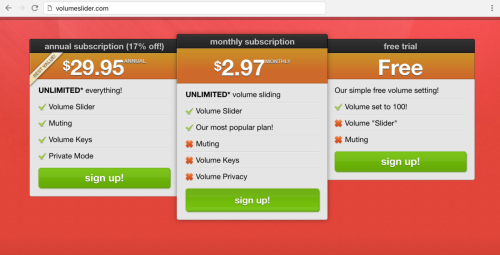
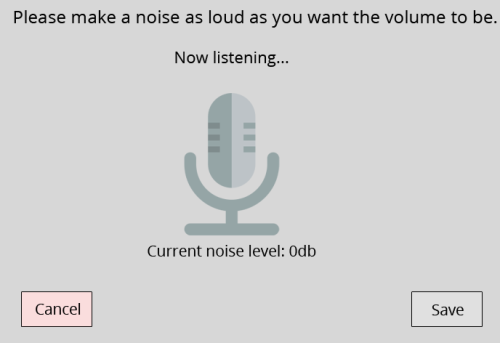
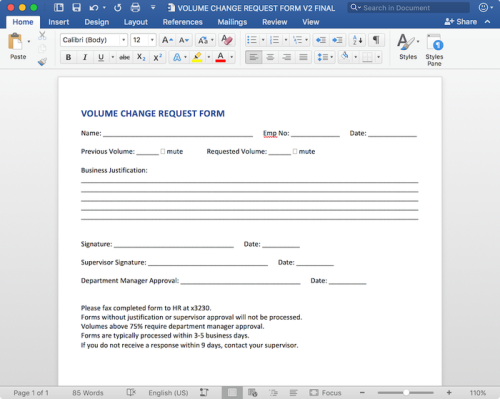
So the exponential function is given by

which evaluated at a real number x gives you the value eˣ, hence the name. There are various ways of extending the above definition, such as to complex numbers, or matrices, or really any structure in which you have multiplication, summation, and division by the values of the factorial function at whatever your standin for the natural numbers is.

For a set A we can do some of these quite naturally. The product of two sets is their Cartesian product, the sum of two sets is their disjoint union. Division and factorial get a little tricky, but in this case they happen to coexist naturally. Given a natural number n, a set that has n! elements may be given by Sym(n), the symmetric group on n points. This is the set of all permutations of {1,...,n}, i.e. invertible functions from {1,...,n} to itself. How do we divide Aⁿ, the set of all n-tuples of elements of A, by Sym(n) in a natural way?

Often when a division-like thing with sets is written like A/E, it is the case that E is an equivalence relation on A. The set of equivalence classes of A under E is then denoted A/E, and called the quotient set of A by E. Another common occurence is when G is a group that acts on A. In this case A/G denotes the set of orbits of elements of A under G. This is a special case of the earlier one, where the equivalence relation is given by 'having the same orbit'. It just so happens that the group Sym(n) acts on naturally on any Aⁿ.

An element of Aⁿ looks like (a[1],a[2],...,a[n]), and a permutation σ: {1,...,n} -> {1,...,n} acts on this tuple by mapping it onto (a[σ(1)],a[σ(2)],...,a[σ(n)]). That is, it changes the order of the entries according to σ. An orbit of such a tuple under the action of Sym(n) is therefore the set of all tuples that have the same elements with multiplicity. We can identify this with the multiset of those elements.

We find that Aⁿ/Sym(n) is the set of all multisubsets of A with exactly n elements with multiplicity. So,

is the set of all finite multisubsets of A. Interestingly, some of the identities that the exponential function satisfies in other contexts still hold. For example, exp ∅ is the set of all finite multisubsets of ∅, so it's {∅}. This is because ∅⁰ has an element, but ∅ⁿ does not for any n > 0. In other words, exp 0 = 1 for sets. Additionally, consider exp(A ⊕ B). Any finite multisubset of A ⊕ B can be uniquely identified with an ordered pair consisting of a multisubset of A and a multisubset of B. So, exp(A + B) = exp(A) ⨯ exp(B) holds as well.

For A = {∗} being any one point set, the set Aⁿ will always have one element: the n-tuple (∗,...,∗). Sym(n) acts trivially on this, so exp({∗}) = {∅} ⊕ {{∗}} ⊕ {{∗∗}} ⊕ {{∗∗∗}} ⊕ ... may be naturally identified with the set of natural numbers. This is the set equivalent of the real number e.

you know girls can tell when you look at their boobs

i don’t care how quickly you glance, 1 second is like 5 seconds in boob time

so, for relativistic boobtime, where t is the observer, and t’ is the time measured at the boob. t=t’/sqrt(1-(v/c)^2) solving for t=1, and t’=5, we get that the boobspeed, v, is represented by v=+/- (6*10^8)sqrt(6)i m/s

boobs travel at 1.5 gigametres per second in the complex direction.

omg that sounds so cool

one of my friends found radiooooo which is a site that streams music from any country from any decade (well, most countries/decade combos work) and we’ve been digging going on a quest to find what is rad

so far the following is good

50s/60s/70s/80s russia

70s cambodia

20s japan

80s ethiopia

80s india

Hello, dear! 🌻

I saw your post wanting book recommendations. I'm sorry for your previous struggles, but I hope this list may help you find something you love!

-"The Housekeeper and the Professor" by Yōko Ogawa (The professor is a mathematician!)

-if you like Vonnegut, you may like Haruki Murakami, specifically his older titles like "Wind-Up Bird Chronicle" and "Norwegian Wood" (I feel these books do a good job of expanding on people's motivations and moods.)

-"The Elegance of the Hedgehog" by Muriel Barbery (Again, excellent at conveying emotions.)

-"Hunting and Gathering" by Anna Gavalda (This one is technically a romance - a genre which I personally would normally HATE - but it portrays such realistic characters, their struggles and their natural dialogue during fights that it actually felt more like I was reading about a collection of lives that I had the pleasure of spying on from above. I really love this book!)

-for WWI and WWII-themed titles, I'd recommend the Battlefield comics by Garth Ennis (He's SO good at writing believable characters and realistic dialogues.)

-if you don't mind high fantasy, any of the books in Terry Praychett's Discworld series about the wizards might be up your alley (You can read them independently without issue, or start from the beginning of any of the wizard titles. You can find a reading guide online! The wizards of his world are very regimented about how magic works - somewhat like mathematicians - and it's very funny.)

-the "Cemetery of Forgotten Books" series by Carlos Ruiz Zafón (I'd skip the 4th one - the main character/POV changed and I wasn't as impressed with the writing in that one - but the first 3 books are an absolute dream to read. The characters are so charming, lovable or completely horrifying, it feels like a wonderful foreign mystery series that takes place in 1940s Spain. It was really interesting to try to keep track of such a unique mystery amidst the second world war.)

I hope those help! Please enjoy your reading journey. ♡

hi, and thank you so much for the recommendations! I appreciate it a lot, those books sound really good